Question
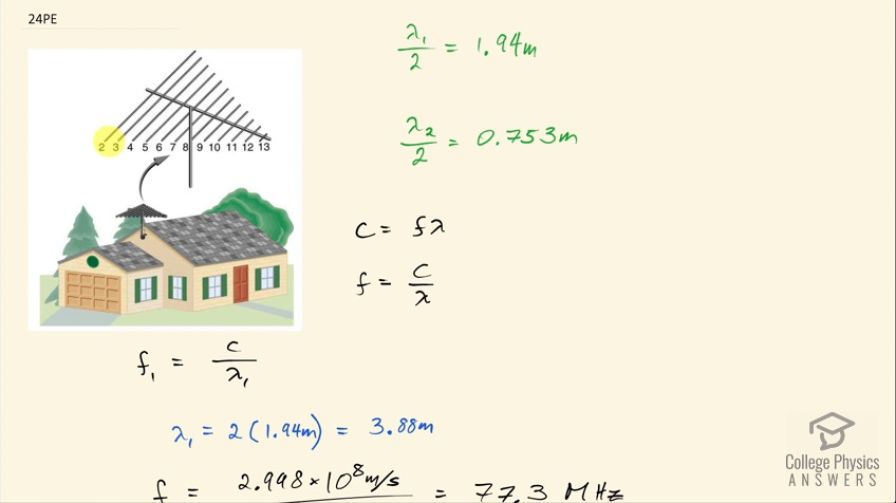
TV-reception antennas for VHF are constructed with cross wires supported at their centers, as shown in Figure 24.27. The ideal length for the cross wires is one-half the wavelength to be received, with the more expensive antennas having one for each channel. Suppose you measure the lengths of the wires for particular channels and find them to be 1.94 and 0.753 m long, respectively. What are the frequencies for these channels?
<b>Figure 24.27</b> A television reception antenna has cross wires of various lengths to most efficiently receive different wavelengths.
Figure 24.27 A television reception antenna has cross wires of various lengths to most efficiently receive different wavelengths.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

77.3 MHz≤f≤199 MHz77.3\textrm{ MHz}\le f \le 199\textrm{ MHz}

Solution video

OpenStax College Physics, Chapter 24, Problem 24 (Problems & Exercises)

OpenStax College Physics, Chapter 24, Problem 24 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 24, Problem 24 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 24, Problem 24 (PE) calculator screenshot 2
Video Transcript
This is College Physics Answers with Shaun Dychko. An antenna is designed so that these horizontal portions of metal have a length that is half the wavelength that it's trying to receive so it's resonating because it has a wavelength half of the incoming wavelength that it's meant to pick up so this must be channel 2, channel 3... and up to channel 13. So we have at the upper end of the length is a length of 1.94 meters so that is λ 1—we'll call it—divided by 2 because this length is half of the wavelength it's meant to receive. And at the short end, is a length of 0.753 meters and we'll call that λ 2 divided by 2. The wave equation tells us that the speed of the light equals its frequency multiplied by its wavelength and we can solve for frequency by dividing both sides by λ because we want to know what are the range of frequencies that this antenna is designed to receive. So frequency at one end of the range is going to be c divided by λ 1, λ 1 being 2 times 1.94 meters, which is 3.88 meters because we rearrange this to solve for λ 1 and multiplying both sides by 2, we get that λ 1 equals 2 times 1.94. So then f 1 then is the speed of light— 2.998 times 10 to the 8 meters per second— divided by this wavelength— 3.88 meters—and that's 77.3 megahertz. The other end of the spectrum for the wavelength is λ 2 and that's 2 times 0.753 meters, which is 1.506 meters. So f 2 then is that speed of light divided by 1.506 meters, which is 199 megahertz. And so the frequencies that this antenna is designed to receive are anything between 77.3 megahertz and 199 megahertz.