Question
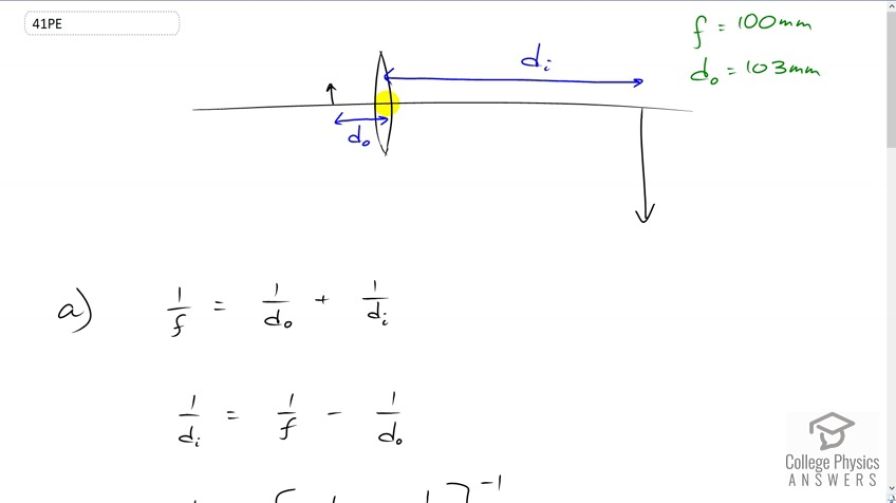
A certain slide projector has a 100 mm focal length lens. (a) How far away is the screen, if a slide is placed 103 mm from the lens and produces a sharp image? (b) If the slide is 24.0 by 36.0 mm, what are the dimensions of the image? Explicitly show how you follow the steps in the Problem- Solving Strategy for lenses.
Final Answer
- ,
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 41 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a thin lens with a focal length of 100 millimeters and our object is placed at 103 millimeters from the lens. And the question is where will the image be? Because that's where one would place the projection screen and it's going to be an inverted and magnified image. So in other words the question is what is di? So we use the thin lens equation and we're going to solve it for di so we'll subtract one over d naught from both sides. And we have one over image distance is one over focal length minus one over object distance and then we'll take the reciprocal of both sides so the image distance then is one over the focal length minus one over the object distance and then take that difference to the power negative one. So that's one over 100 millimeters minus one over 103 millimeters all to the negative one which gives 3433 and make sure you notice that since I plugged in millimeters into the equation here our answer is also in millimeters and we'll multiply that by one meter for every thousand millimeters and get 3.43 meters. So that's the distance that the screen should be from the lens on the other side compared to the object. Now we want to figure out what the dimensions of the image will be given the known dimensions of the object. So magnification which is the image height divided by the object height we know is the negative of the image distance divided by the object distance and so we'll find the image height by multiplying both sides by the object height that we know and then we solve for hi and it’s object height times negative image distance divided by object distance. And we know this image distance and object distance. So that's negative 3.433 meters divided by 103 times ten to the minus three meters. This is the object distance. And this gives a height in the image of negative 33.33 multiplied by whatever the object dimension is. So we’ve found the magnification in other words and then we use that to figure out the length and width of the image. Now we don't really care about the negative sign here, the fact that it's inverted, so it does take the absolute value of that magnification. So the length of the image is going to be 33.33 times 24 millimeters. And that's going to work out to this many millimeters which we multiply by one meter for every thousand millimeters giving length that 0.8 meters. And then the width will be 33.33 times 36 millimeters giving an image width of 1.20 meters.

