Question
You can determine the index of refraction of a substance by determining its critical angle. (a) What is the index of refraction of a substance that has a critical angle of when submerged in water? What is the substance, based on Table 25.1? (b) What would the critical angle be for this substance in air?
Final Answer
- . This is fluorite.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 25 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
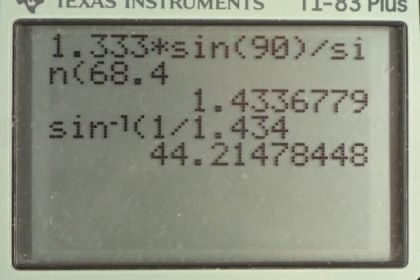
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Some unknown substance is submerged in water and we measure the critical angle. So, a beam of light is starting in the substance and then reaches this interface between the substance and water and the angle of refraction is 90 degrees parallel to this interface when you're at the critical angle. And then using this critical angle, and the fact that we're in water, and we know the index of refraction of water, we'll figure out what the index of refraction of this unknown substance is. And then, look up in table 25.1, figure out what the substance must be given this index of refraction that we find. So, Snell's law says that the initial index of refraction times sine of the angle of incidence equals the second index of refraction times sine of the angle of refraction. So in this case, the angle of incidence is theta c, the critical angle, and the angle of refraction is 90 degrees. So theta two is 90. And n two is the index of refraction of the second medium, which in this case is water because we're told it's submerged in water, and it has an index of refraction of 1.333. So, we divide both sides by sine of the angle of incidence. And, so have n one equals n two sin theta two over sin theta one, and then I substitute in theta c, is what we really should be calling this theta one, this angle of incidence is the critical angle in this case, and the angle of refraction is 90 degrees when the angle of incidence is the critical angle. And so n one then is 1.333, index of refraction of water, times sine of 90, divided by sine of 68.4 degrees. And that makes 1.43 is the index of refraction of this material. And so, it must be fluoride, when you look up in the data table: different materials having different indices of refraction. Now, if this was submerged in air — you know, see, you don't really say 'submerged' in air, but air is a fluid, you can argue so... whatever — but it's in air, and what would the critical angle be? Well, I could write sine of 90 here, but sine of 90 is just one so that's why I just wrote n two. And we have n one, which we now know is 1.43 times sine of the critical angle, and we're gonna solve this for theta c now. So divide both sides by n one, then take the inverse sine of both sides, and you get the critical angle is the inverse sine of the second index of refraction divided by the first index of refraction. of the second index of refraction divided by the first index of refraction. So, it's the inverse sine of air, index of refraction of air, which is one, and divide that by the index of refraction of fluoride, 1.434, and this gives a critical angle of 44.2 degrees.