OpenStax College Physics for AP® Courses, Chapter 25, Problem 50 (Problems & Exercises)

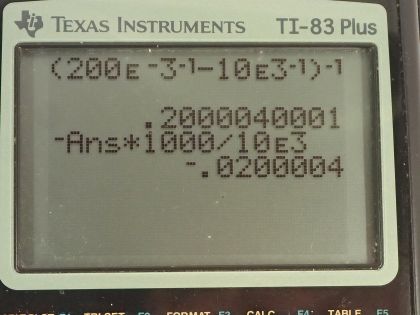
This is College Physics Answers with Shaun Dychko. We suppose that a 200 millimeter focal length lens is being used to photograph some mountains that are 10.0 kilometers away so the distance between the lens and the mountains is the object distance d o and that's 10.0 times 10 to the 3 meters and the focal length is 200 times 10 to the minus 3 meters. The question in part (a) is where will the image be? So we need to use the thin lens equation which says that 1 over object distance plus 1 over image distance equals 1 over focal length and we'll subtract 1 over d o from both sides and then we get 1 over d i on the left equals 1 over focal length minus 1 over d o on the right and I prefer to write this 1 over f as f to the power negative 1 and so we have f to the negative 1 minus d o to the negative 1. Then we raise both sides of this equation to the exponent negative 1 and the left side becomes d i for image distance and the right side is f to the negative 1 minus d o to the negative 1 all to the negative 1 and this negative 1 business is more convenient because there's a single button on the calculator that just does negative 1 exponent. So we have 200 times 10 to the minus 3 meters to the negative 1 minus 10 times 10 to the 3 meters to the negative 1 and then that result is raised to exponent negative 1 and we get 0.200 meters, which we can convert into centimeters by multiplying by 100 centimeters for every meter and we get 20.0 centimeters is the distance between the lens and the image and so the film in the camera should be this distance away from the lens. Part (b) is asking what is the height of the image of a 1000 meter high cliff on one of the mountains? So we need to use this magnification formula that says that the image height divided by the object height equals negative of the image distance divided by the object distance. So the object height is what's given to us— this 1000 meter height of the cliff— and we'll multiply both sides by h o to solve for h i. So h i then is the negative of the image distance times the object height divided by the object distance. So that's negative 0.200004 meters keeping lots of digits because this is an intermediate calculation— that's the image distance— multiplying it by height of the cliff—1000 meters— divided by the distance between the lens and the cliff, which is 10.0 times 10 to the 3 meters and that is negative 0.0200 meters, which is negative 2.00 centimeters. This negative sign just means that the image is inverted compared to the object so it will be flipped upside-down but its absolute size is 2.00 centimeters high.