Question
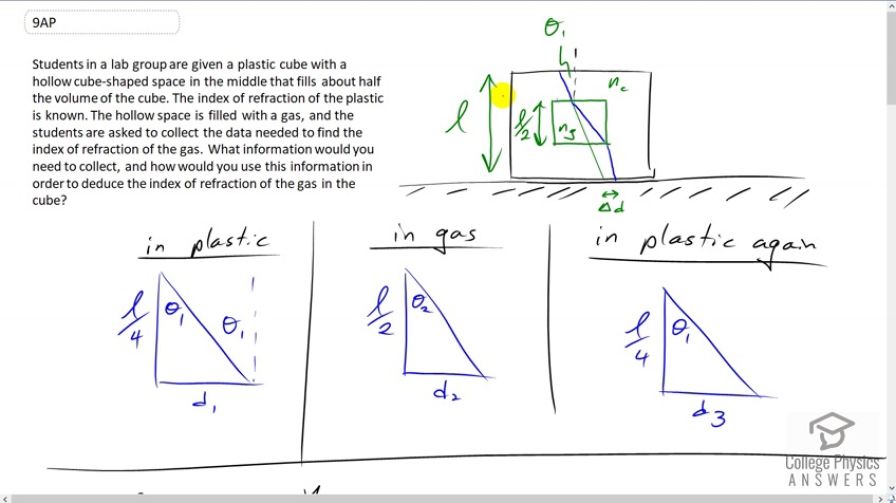
Students in a lab group are given a plastic cube with a hollow cube-shaped space in the middle that fills about half the volume of the cube. The index of refraction of the plastic is known. The hollow space is filled with a gas, and the students are asked to collect the data needed to find the index of refraction of the gas. What information would you need to collect, and how would you use this information in order to deduce the index of refraction of the gas in the cube?
Final Answer
data needed: \Delta d\textrm{n}_c\Delta d$.
Solution video
OpenStax College Physics for AP® Courses, Chapter 25, Problem 9 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We're given a plastic cube with a known index of refraction we’ll call n subscript c for Cube and it has a known height we’ll call that l. And inside of it is a cube full of gas with an unknown index of refraction n subscript g and this Cuban side has a height which is half that of the outer Cube. So we'll call this inner Cube l over two for its height and we're going to have a ray of light that goes at a known angle of incidence will call it Theta one here and then we'll figure out by how much this Ray is displaced here compared to if the cube was not there compared to this straight line that would go here if the gas was not present to displace the ray. So we're going to measure Delta d, Theta one, index refraction of the cube and the cubes height and knowing that we'll be able to figure out the index of refraction of the gas. So how we're going to do that is first consider this picture where we have in the plastic compared to this point here, the beam will get displaced distance d1 by the time it gets to the top of the gas Cube. And then in the gas is going to get displaced an amount d2. And then in the plastic again, it's going to get displaced an amount d3 here. And so this leg of the triangle is l over four, that's the distance here and that first triangle above the gas Cube and then within the gas Cube, we have a distance of l over two. And then in the plastic again, we have a distance l over four. And so we're going to compare this total distance of d1 plus d2 plus d3 with the distance, if you had no gas ng for no gas. And so, you know, it's going to go add an incident angle Theta One have the entire distance l the tire height of the plastic Cube and we can figure out dng by saying that the tangent of this angle Theta One is the opposite over the adjacent. And so that's d no gas divided by l and we'll multiply both sides by l . To solve for distance of with no gas l times Tan Theta One. And then we're going to take the difference between that and the total distance when there is gas. So we have these portions d1 and d3 within the plastic and those parts are straightforward to calculate and in each case is going to be Theta One is going to be the opposite d1 or d3 and then tangent of that is going to be that horizontal displacement divided by l over four. And so d1 is l over four times Tan Theta One and now this part for calculating d2 is a bit more involved. So this triangle has faded two here. This is an angle of refraction when it goes through the into the gas and we know that from Snell's law that the index refraction of the cube times sine Theta One is going to equal the index of refraction of the gas times sine Theta two . And we can solve for Theta two by dividing both sides by ng. And then taking the inverse sine of both sides. So Theta two inverse sine of nc sine Theta One over ng and that is something that we can plug into the tangent. So we're going to go d2 is l over two times tangent of Theta two . But Theta two is all of this and so that's where that comes from. So the total with the gas is D1 plus d2 plus d3 , butd3 equals d1 . Because once this beam returns back to the same plastic material of the cube, it's going to return to the same angle here Theta One that is started with up here. And so d3 down here is going to equal d1 up there. And so that's two d1 plus d2 and so that's two times l over four times Tan Theta One plus l over two times Tan of inverse sine nc sine Theta One over ng and this Delta d that we can measure is going to be the difference between the distance with no gas l times Tan Theta One minus all of this. And then we can factor out the l over two here and we get Delta d then is l over two times tan Theta One minus tan of the inverse sine of nc times sine of Theta One over ng. Now this formula we really hard to I don't think you can solve it analytically, you need to use a spreadsheet and solve this numerically to figure out what ng if you keep plugging in different possible possibilities for ng what ng would give you the Delta d that you measure given all these other things that you've also measured and so we solve this numerically and the data we need is the height of the cube, the incident angle, the displacement of the beam with no gas compared to with gas, and the index of refraction of the cube material.