OpenStax College Physics for AP® Courses, Chapter 27, Problem 58 (Problems & Exercises)

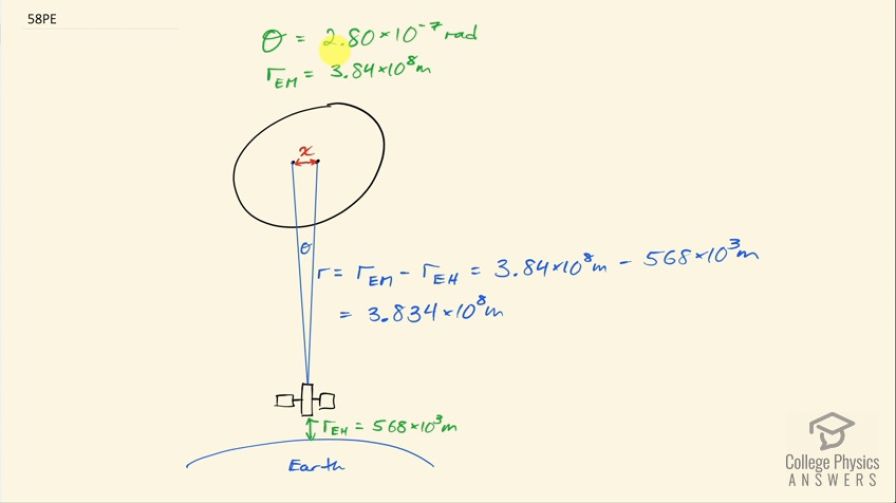
This is College Physics Answers with Shaun Dychko. In example [27.5], we are told that this minimum Rayleigh Criterion angle is 2.80 times 10 to the minus 7 radians. So we know that that's what this angle is here between these two spots that are on the moon we want to know what is this minimum distance that we can possibly have between these two objects in order for them to be distinguishable by the Hubble telescope? We have this Hubble telescope at an Earth-Hubble distance 568 kilometers above the surface of the Earth and we also know what the Earth-Moon distance is— 3.834 times 10 to the 8 meters— and that means this distance between the Hubble and the Moon is the difference between the Earth-Moon and the Earth-Hubble distance this works out to 3.834 times 10 to the 8 meters. Okay! So we need to know that distance because this separation between the objects— we'll call it x— approximately equals this angle times this Hubble-Moon distance. Strictly speaking, this formula Θ times r tells you the arc length on this edge of this circle that we could imagine being here. So this arc length s is exactly Θ times r, where Θ has to be measured in radians because that's what Θ is when you talk about units of radians, it is the arc length divided by the radius of a circle. But with such a small distance, and if you were to like imagine zooming in on a little portion of this arc length, it would appear to be straight pretty much and so that's what we are saying here is that this straight line distance between these two points is approximately the same as the arc length given such a small angle. Okay! So that means we can take the angle— 2.80 times 10 to the minus 7 radians— multiply it by the distance between the Hubble and the Moon— 3.834 times 10 to the 8 meters— and that makes a minimum separation between objects on the Moon of 107 meters.