Question
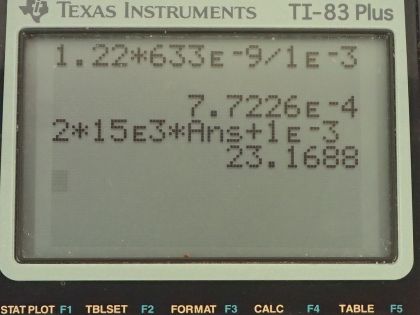
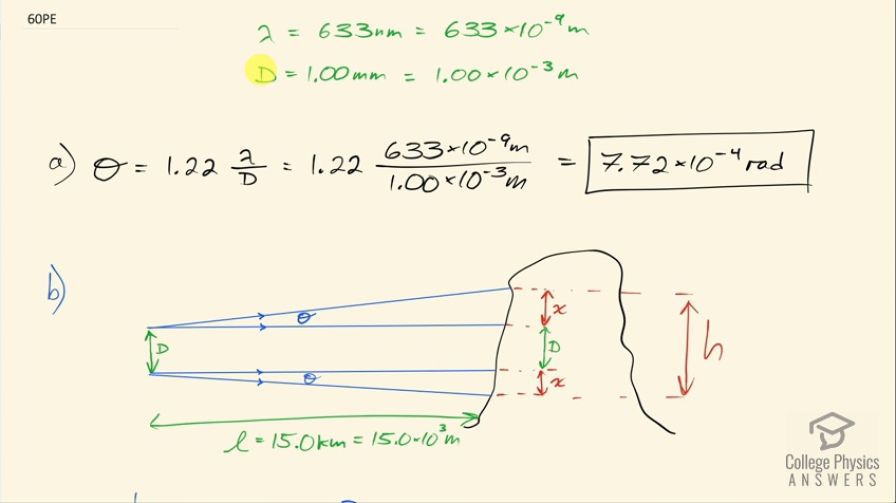
(a) What is the minimum angular spread of a 633-nm wavelength He-Ne laser beam that is originally 1.00 mm in diameter?
(b) If this laser is aimed at a mountain cliff 15.0 km away, how big will the illuminated spot be?
(c) How big a spot would be illuminated on the Moon, neglecting atmospheric effects? (This might be done to hit a corner reflector to measure the round-trip time and, hence, distance.) Explicitly show how you follow the steps in Problem-Solving Strategies for Wave Optics.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 60 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We imagine that we have a Helium-Neon laser that has a wavelength of 633 nanometers being projected out of an aperture of size 1.00 millimeter and we want to know what is the minimum angular spread due to diffraction of this beam. So the angular spread is 1.22 times the wavelength divided by the diameter. We need the units of λ and D to be the same so we convert them both into meters. So we have 633 times 10 to the minus 9 meters divided by 1.00 times 10 to the minus 3 meters times 1.22 times and this is 7.72 times 10 to the minus 4 radians and notice that our answer is in radians when we use this formula. Part (b) is asking if this laser is aimed at a mountain cliff that's 15.0 kilometers away, how big will this spot be? So this angular spread occurs on both the top and the bottom of the laser beam and this is the original central spot of size 1.00 millimeter and then once it reaches this mountain cliff— that is 15.0 kilometers away— it's going to be spread out because there's going to be this spread at the top—we will call that distance x— and then the spread also at the bottom— another distance x— for a total height of this spot, which is going to be 2 times x plus the original central beam of size D. So let's figure out what x is. This distance l here, we consider to be part of a radius of a circle and then this distance x is like the arc length at the end of this imaginary circle and the arc length, which we could call s would be this radius l times the angle Θ in radians but with such a small angle, we can also say that the straight line distance the cord so to speak between this point and this point is approximately the same as the arc length so that's what we are seeing here with this approximately equal business is that this straight line distance is approximately the same as what the arc length would be between here and here and that is the radius times the angle. Okay! Because this is what radians means by the way an angle in radians is the arc length divided by the radius so if you have a circle and you have some sector here and this is the arc length along the perimeter s and the circle has some radius r, the meaning of Θ when expressed in radians is this arc length divided by the radius. Okay! And that makes s equal to r times Θ, which is what I am saying here and this distance x is approximately the same as the arc length. Okie-doke... hopefully, I didn't belabor that point too much but anyway... wanted to make that clear! So h then is 2 times l times Θ plus D that is 2 times 15.0 kilometers, expressed in meters, and then multiply by the angular spread that we determined in part (a) plus the aperture size and this works out to 23.2 meters. In part (c), it's the same kind of question but now the distance is from the Earth to the Moon which is 3.84 times 10 to the 8 meters so we plug in that number instead of 15.0 kilometers and everything else otherwise is the same and we get a spot size of 593 kilometers.