OpenStax College Physics for AP® Courses, Chapter 27, Problem 81 (Problems & Exercises)

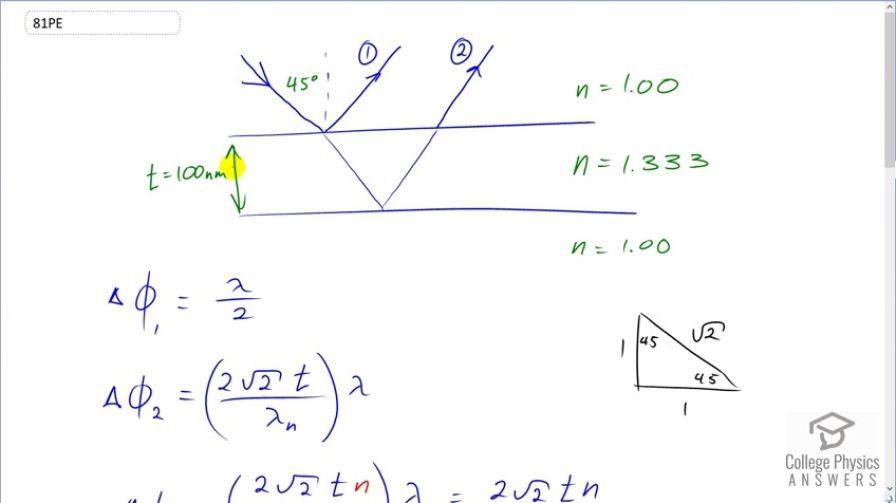
This is College Physics Answers with Shaun Dychko. White light is incident on this soap film at an angle of 45 degrees. The soap film is 100 nanometres thick and has index of refraction same as that of water which is 1.333 and the question is asking that which wavelength of light will experience constructive interference. So, which color will we see in other words. So, we have reflection of this interface between the air and water and because it’s going from medium with low index of refraction 1.0 to medium with high index of refraction 1.333, this refraction will automatically cause a phase shift of half a wavelength, lambda over two and ray two on the other hand will be reflected off of this interface but its beginning in the medium with a high index and reflecting off of interface where the second medium is of low index of refraction, because this is air on the inside of the bubble and so there will no phase shift resulting from a reflection but there will be a phase shift due to the increased distance that this ray number two travels and so we will figure out an expression for that in a second. Now, down here we are going to see that the total phase shift has to equal some integer times the wavelength where m is one, two, three or so on and we are gonna solve for what this wavelength is. Now, let’s figure out what the phase shift for ray two is. So, ray two is traveling along this hypotenuse of this triangle here and this right triangle is a special triangle because it has 45 degrees angles in here and we can draw that triangle and write down what the corresponding sides are. So, if this leg was one and this leg was one then the hypotenuse would be root two because it’s the square root of the sum of the squares of each of the legs. You could instead put sine 45 to your calculator and multiply that by one of the legs and that would also give you the hypotenuse, that may give you 1.4, 14, whatever square root two is but I like to use this special triangle. So, we have a… we have this hypotenuse of length, thickness, times root two because this thickness is corresponding to this leg here and we multiply that whatever that is, we multiply it by root two to get the length of hypotenuse and then we are doing that twice because we are going once here and then once again back up. So, we have two root two times the thickness is the distance that the ray is traveling but what we want to know is the number of wavelengths it has traveled and so we divide this distance by the wavelength which is the wavelength in the medium, so I have a subscript ‘n’ there to say the wavelength in the soap film and lambda n is the wavelength in a vacuum or air divided by the index of refraction and so when dividing by lambda over n, we are gonna instead multiply by the reciprocal of that which is n over lambda. So, we have this number of wavelengths and then we multiply by the number of nanometres per wavelength to get the number of nanometres of phase shift of the ray two and that’s gonna be two root two times the thickness times the index of refraction of the soap film. So, the total phase shift is gonna be sum of the phase shifts of waves one and two. So, that’s lambda over two plus two root two, thickness times index of refraction equals some integer times lambda for constructive interference. Then we multiply both sides by two to get rid of the fraction. So, we have lambda plus four root two, t n equals two m lambda and then I’ll subtract lambda from both sides and then switch the sides around to have the unknown lambda on the left and then we get this line here and we will factor out the common factor lambda. So, we have lambda bracket two times this integer m minus one equals four root two t n and then divide both sides by two m minus one and we get to the wavelength which will experience constructive interference is four root two t n over two m minus one. Now, we can choose what m is and we can see if the result is visible color. So, let’s start with number one and so we have four root two times 100 nanometres thickness times index of refraction of the soap which is 1.333 divided by two times one minus one which gives 754 nanometres, and this is a visible wavelength. It’s a color red and so this film will appear red when viewed at an angle of 45 degrees.