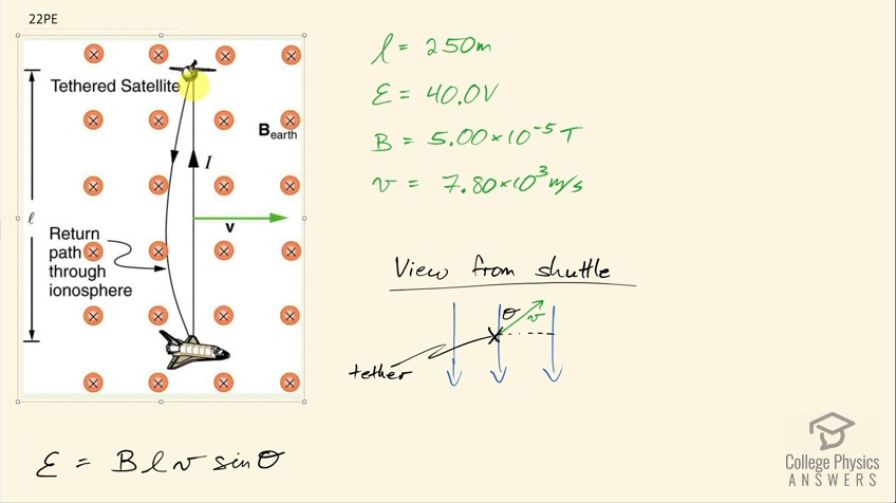
Question
In the August 1992 space shuttle flight, only 250 m of the conducting tether considered in Example 23.2 could be let out. A 40.0 V motional emf was generated in the Earth’s 5.00×10−5 T5.00\times 10^{-5}\textrm{ T} field, while moving at 7.80×103 m/s7.80\times 10^{3}\textrm{ m/s} . What was the angle between the shuttle’s velocity and the Earth’s field, assuming the conductor was perpendicular to the field?
Question by OpenStax is licensed under CC BY 4.0
Final Answer

24.2∘24.2^\circ

Solution video

OpenStax College Physics for AP® Courses, Chapter 23, Problem 22 (Problems & Exercises)

OpenStax College Physics, Chapter 23, Problem 22 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 23, Problem 22 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. In 1992, the space shuttle deployed a 250 meter length of tether to this satellite after which the tether jammed and they couldn't deploy it any further but they did collect some data when they did at least this much and they ended up finding that there's a 40.0 volt emf induced given the Earth's magnetic field of 5.00 times 10 to the minus 5 tesla while the shuttle was moving at 7800 meters per second. So the question is what angle with respect to the magnetic field direction is the velocity given all of this information? So we want to know what is the component of the velocity that is perpendicular to the magnetic field so this is v subscript perpendicular and that is v times sin of Θ because this is the opposite leg of this right triangle. So we multiply sin Θ by the hypotenuse to get this opposite leg and that's what I have here. So the induced emf is the magnetic field strength due to the Earth times length of the tether times the component of velocity perpendicular to magnetic field. So we can solve for sin Θ by dividing both sides by Blv and we have sin Θ is the induced emf divided by the magnetic field strength times the length of the tether times the speed of the shuttle and we'll take the inverse sin of both sides and so we have Θ then is inverse sin of emf over Blv so the inverse sin of 40.0 volts divided by 5.00 times 10 to the minus 5 tesla times 250 meters times 7.80 times 10 to the 3 meters per second and that is 24.2 degrees.