Question
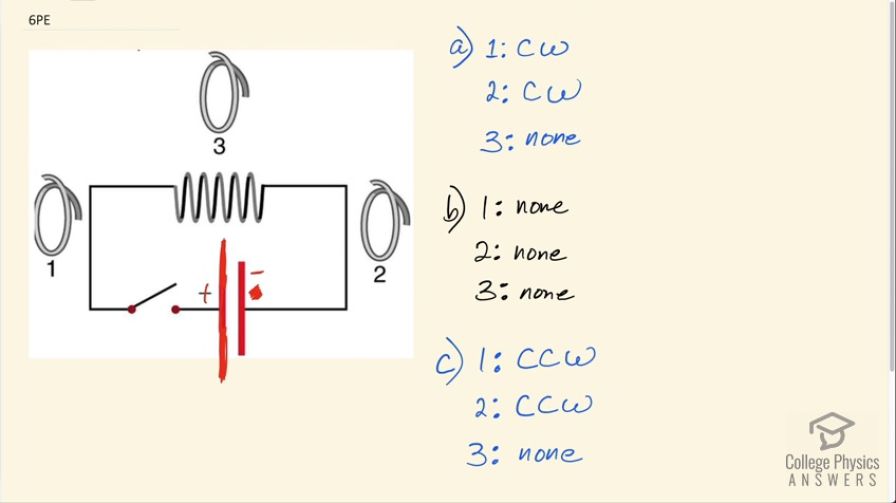
Referring to Figure 23.58, but reversing the direction of the battery, what are the directions of the currents in coils 1, 2, and 3 (assume that the coils are lying in the plane of the circuit): (a) When the switch is first closed? (b) When the switch has been closed for a long time? (c) Just after the switch is opened?
Final Answer
- 1: CW, 2: CW, 3: none
- 1: none, 2: none, 3: none
- 1: CCW, 2: CCW, 3: none
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 6 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a battery with a positive terminal here—the long bar— and a negative terminal here and this means the current is going to the left when the switch is closed then it goes up the left side and to the right along the top branch and then down on this right side. So in part (a), we are told that the switch is first closed and what will be the direction of the induced current in coils 1, 2 and 3? So initially before the switch is closed, there's no current and therefore no magnetic field externally through this coil and when I say externally, I mean the field produced by this wire is external to the coil and when the switch is closed with the current going up here, there now is a magnetic field produced by the wire in the coil and that field will be... it will have a direction depending on the right hand rule so we'll grab this portion of wire with our right hand thumb pointing upwards in the direction of the current and at the position of this coil, our fingers are coming out of the page so we can draw dots to represent the field produced by this wire... the current in this wire. Now the induced magnetic field is going to oppose this change in flux; there's now a flux coming out of the page through this loop as a result of this magnetic field that's been introduced and so it will oppose it by having a magnetic field that is going into the page because it's going to try and sort of achieve its original no-flux state by opposing this new, external field out of the page and to have a field that's induced into the page requires a current that is going counter-clockwise— maybe I'll put it in red... counter-clockwise— and you can figure that out by pointing your fingers in the loop down into the page I should say and then grab the wire say at the bottom here and your thumb will be pointing to the left and likewise, if you go to the top of the wire or this loop fingers into the page, your thumb will be pointing to the right. So clockwise induced current, when the switch is closed. In loop 2, initially there's no magnetic field through the loop and then when the switch is closed, we have this current going down in this wire if you grab this wire with your right hand, thumb pointing down, your fingers are coming out of the page as a result of this current in the wire and it's the same analysis as it was for loop 1, we now have a flux coming out of the page and so the induced magnetic field will oppose that change by going into the page and that requires a current that is clockwise. Loop 3 has no induced current because there's no change in flux through the loop because this wire is in this solenoid shape and if you were to grab this portion of wire here with your right hand, the current is going out of the page here and with your fingers... or sorry... with your thumb grabbing this piece of the solenoid, thumb coming out of the page your fingers are pointing directly to the left so the magnetic field produced by this portion of the solenoid closest to the loop is going to the left, which is parallel to the plane of the loop and so it does not create any flux. And you could examine this magnetic field produced by this portion of the solenoid, your thumb would be pointing into the page and then your fingers would be pointing to the right and so there would be a slightly less strong magnetic field being directed to the right here as a result of this side of the solenoid. So in all this, there's going to be a net field pointing to the left because this field due to this side of the solenoid will be stronger but it's going to be weak and furthermore, it's parallel to the plane of this loop so there's no change in flux— there's no flux at all— and so there's no induced current. That will be the same for loop 3 and all of our parts here because... yeah. So part (b) says that the switch has been closed for a long time which means there's no change now in the flux through the loops and so there will be no induced current then and so the answer is none for all of them. And part (c) we are told that the switch, after having been closed for a long time, is then opened and when that happens, there was originally... a flux coming out of the page in loop 1 and then that's going to be reduced when the switch is opened and so the induced magnetic field will try to replace what's now missing so it will be coming out of the page to replace what it once had opposing the change, in other words, and so to have a magnetic field induced coming out of the page in the loop, the current has to be going this direction here— it has to be going counter-clockwise— and you can find that out by pointing your fingers up in the middle of the loop and your thumb will be pointing in the counter-clockwise direction. The analysis is the same for loop 2: initially, the field lines are coming out of the page and then when the switch is opened, the field coming out of the page will reduce and therefore, it will have a reduced flux out of the page and so the induced magnetic field will try to hold on to what it once had try to oppose this reduction by providing its own magnetic field out of the page and that is a counter-clockwise current again and loop 3 still has no flux through it. There we go!