Question
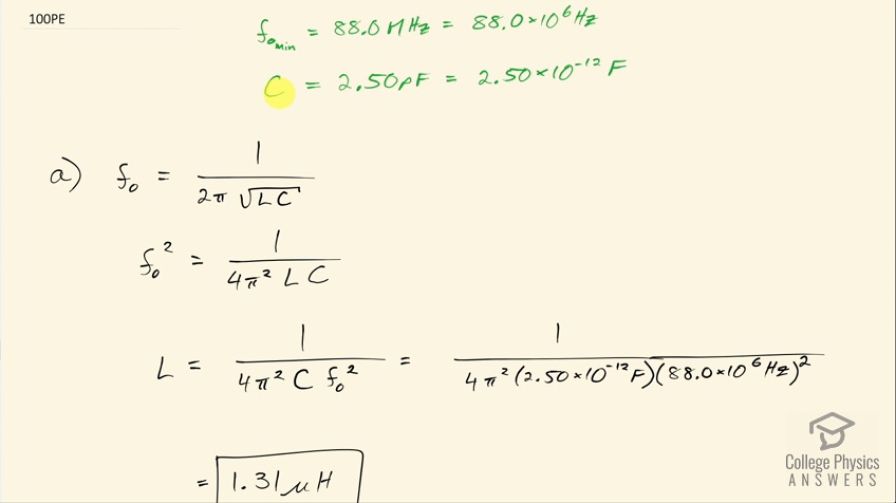
The lowest frequency in the FM radio band is 88.0 MHz. (a) What inductance is needed to produce this resonant frequency if it is connected to a 2.50 pF capacitor? (b) The capacitor is variable, to allow the resonant frequency to be adjusted to as high as 108 MHz. What must the capacitance be at this frequency?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 100 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A FM radio receiver has a minimum resonant frequency of 88.0 megahertz which is 88.0 times 10 to the 6 hertz and a capacitance of 2.50 picofarads, which is 2.50 times 10 to the minus 12 farads and the question is what is the inductance of this circuit? So the resonant frequency is 1 over 2π times the square root of inductance times capacitance and we can first square both sides to get resonant frequency squared equals 1 over 4π squared times inductance times capacitance and we can solve for L by multiplying both sides by L over f naught squared. So the inductance then is 1 over 4π squared times capacitance times resonant frequency squared. So that's 1 over 4π squared times 2.50 times 10 to the minus 12 farads times 88.0 times 10 to the 6 hertz squared which is 1.31 microhenries. And in part (b), it's asking us what capacitance would be needed in this second case when we have the maximum possible frequency in the FM band which is 108 megahertz? So we can you know... rearrange this same formula but solve it for C instead of L in which case we would have capacitance then is 1 over 4π squared times inductance times the resonant frequency squared. So this is 1 over 4π squared times the inductance that we found in part (a) times the new frequency—108 times 10 to the 6 hertz squared— and that is 1.66 picofarads.
