Question
To receive AM radio, you want an RLC circuit that can be made to resonate at any frequency between 500 and 1650 kHz. This is accomplished with a fixed inductor connected to a variable capacitor. What range of capacitance is needed?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 23, Problem 96 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
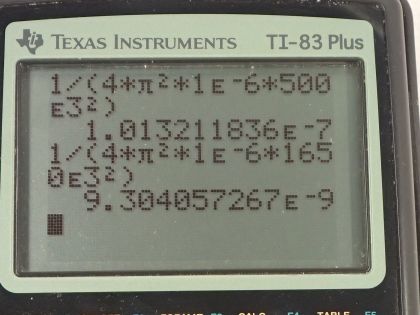
This is College Physics Answers with Shaun Dychko. An AM radio needs its LRC-circuit to resonate from a minimum frequency of 500 kilohertz upto a maximum frequency of 1650 kilohertz and it has an inductor in it with an inductance of 1.00 microhenries. So we need to figure out what capacitance is needed in order to resonate at each of these frequencies? So the resonant frequency of an LRC-circuit is 1 over 2π times the square root of the product of the inductance and capacitance and we can solve this for C by first squaring both sides and we have f naught squared on the left equals 1 over 4π squaredLC on the right and then multiply both sides by C over f naught squared. So the capacitance then is 1 over 4π squared times inductance times the resonant frequency squared. So the first capacitance will be 1 over 4π squared times inductance times the minimum resonant frequency squared so that's 1 over 4π squared times 1.00 times 10 to the minus 6 henries times 500 times 10 to the 3 hertz squared which is 101 nanofarads. The second capacitance needed is 1 over 4π squared times the inductance times the maximum frequency— 1650 times 10 to the 3 hertz squared— and that is 9.30 nanofarads. So the capacitance needs to be variable from a minimum of 9.30 nanofarads upto 101 nanofarads.