Question
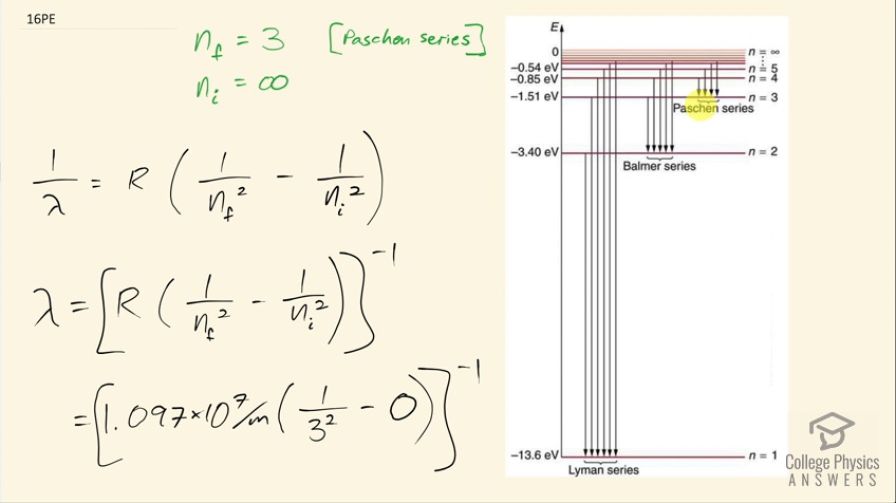
Show that the entire Paschen series is in the infrared part of the spectrum. To do this, you only need to calculate the shortest wavelength in the series.
Final Answer
The shortest wavelength in the Paschen series is , which is greater than the shortest infrared wavelength. This means the entire Paschen series is in the infrared part of the spectrum. (By the way, it might be worth testing whether the longest wavelength emission in the Paschen series, for is actually in the microwave or radio part of the spectrum).
Solution video
OpenStax College Physics, Chapter 30, Problem 16 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In the Paschen series, the final energy state has n equal to 3 and we are meant to show in this question that the entire Paschen series is in the infrared part of the spectrum. So to do that, we will find the shortest possible wavelength and show that even that shortest wavelength still exceeds... is still greater than the shortest infrared wavelength. So we are going to get the shortest wavelength by looking at the transition that results in the highest energy emission and that will happen when n starts from its largest possible initial state before it ends at the final state of n equals 3 and the largest possible initial state is infinity so the electron is basically unbound to the atom and then from that initial state, n's at a state of n equals 3. So this formula here will help us find the wavelength. So 1 over the wavelength that would be emitted in this transition is the Rydberg's constant times 1 over the final value for n squared minus 1 over the initial value for n squared and take the reciprocal of both sides to solve for λ. So we have then that the wavelength at its shortest for the Paschen series is 1.097 times 10 to the 7 per meter times 1 over 3 squared minus 0 because we are having 1 divided by the initial state of infinity squared and this is essentially zero and take all of that to the power of negative 1 and this is 820 nanometers. So that means every wavelength emitted by transitions in the Paschen series are going to be greater than or equal to 820 nanometers but infrared light is everything greater than 750 nanometers so that means the entire Paschen series is in the infrared part of the spectrum.
