Question
Verify that the ground state energy E0E_0 is 13.6 eV13.6\textrm{ eV} by using E0=2π2qe4mek2h2E_0 = \dfrac{2 \pi^2 q_e^4 m_e k^2}{h^2}.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

Please see the solution video.

Solution video

OpenStax College Physics, Chapter 30, Problem 10 (Problems & Exercises)

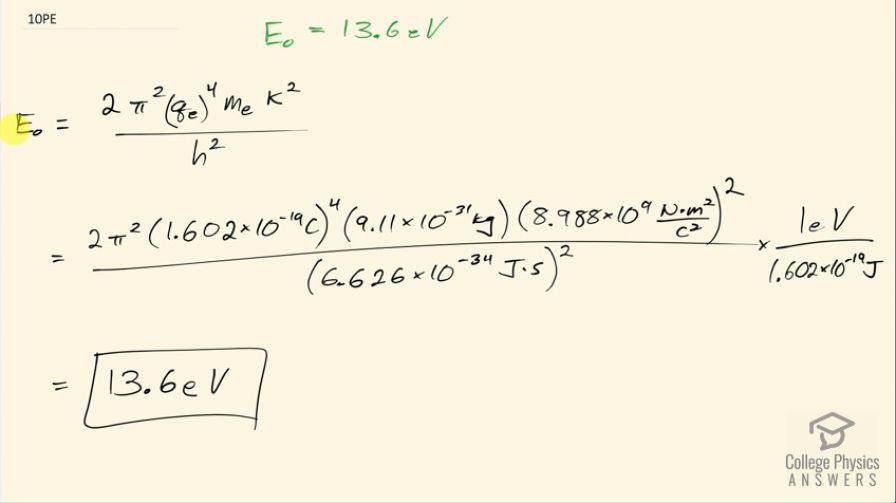
OpenStax College Physics, Chapter 30, Problem 10 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 30, Problem 10 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to confirm that the binding energy of an electron in the ground state of hydrogen is 13.6 electron volts; we are told that the ground state energy has this formula: 2 times π squared times the elementary charge to the power of 4 times the mass of an electron times coulomb's constant squared divided by Planck's constant squared. So we plug in values for each of these constants and then at the end convert from joules into electron volts by multiplying by 1 electron volt for every 1.602 times 10 to the minus 19 joules because this whole thing here will give an answer in joules since we have used mks units in our quantities here. Now for my calculator—your calculator might be different— but for my calculator, I had to change this exponent to a 3 and then not divide by this thing because, you know, 1.602 times 10 to the minus 19 to the power of 4 divided by 1.602 times 10 to the minus 19 is just this number to the power of 3 and I needed to do that because with an exponent 4 here and then multiplying by something times 10 to the minus 31 the calculator just essentially thought the number was zero and it couldn't handle such a small value so in case you are getting zero on your calculator that's a little trick. So the answer is 13.6 electron volts as we expect.

Comments

would this only be the ground state energy for hydrogen? does every element have its own ground state energy?

Hi Ryan, thanks for the question. E0E_0 is the ground state only for hydrogen, whereas other "hydrogen-like" atoms have ground states in terms of E0E_0 of E=−Z2E0E = -Z^2E_0, where I substituted n=1n = 1 for the ground state in equation [30.26] En=−Z2n2E0E_n = -\dfrac{Z^2}{n^2}E_0, and ZZ is the number of protons in the atom. The electron is more tightly bound to nuclei with more protons. Equation [30.26] is pretty limited, however, since it's only for "hydrogen-like" atoms, which means there is only one electron. A better term for them would be "hydrogen-like ions", rather than atoms, since, with the exception of hydrogen, they would all be charged. When additional electrons surround the nucleus (it's no longer a hydrogen-like ion in other words), things get more complicated and there doesn't exist a formula for calculating the ground state energy of the inner-most election in that circumstance. You might find the Wikipedia discussion of ionization energy interesting. The "ground state energy of the hydrogen atom" is the same as the "ionization energy of hydrogen".
All the best,
Shaun