OpenStax College Physics for AP® Courses, Chapter 11, Problem 9 (Problems & Exercises)

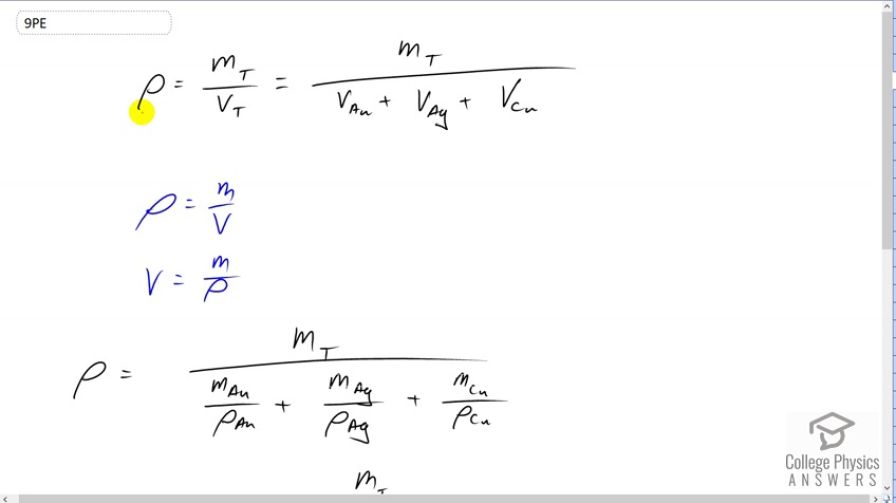
This is College Physics Answers with Shaun Dychko. In this question we're asked to find the density of 18 karat gold. So, 18 karat gold has a mixture of 18 parts gold, five parts silver and one part copper. So its density will be whatever the total mass of the combination is, divided by its total volume. The total volume will be the volume of the gold plus the volume of the silver plus the volume of the copper. The subscripts here are the symbols in the Periodic Table of elements for each of those elements, gold, silver and copper. So, we don't know what the total mass is, nor do we know the volume. But we can express volume in terms of mass given this density formula, mass over volume. We can solve it for V by multiplying by V over rho on both sides. We get V equals mass over density. So we make a substitution for each of the volumes in our density formula up here. So we have the density of this 18 karat gold is the total mass divided by the mass of gold divided by its density, plus the mass of silver divided by silver's density, plus the mass of copper divided by copper's density. So these are each of the volumes of those elements. Then we use the information in the question that says we have 18 parts gold. So of the 24 parts total of this mixture, 18 of them are gold and so we can substitute 18 over 24, that's the fraction of the mass which is gold. So eighteen twenty-fourths of the total mass is gold. Then add to that five parts out of 24 which is silver, and then add to that one over 24 parts which is copper. Each of those masses are of course divided by their respective densities. Now total mass we can see is a common factor on the top and bottom and so it cancels and so that's one on top there. There's a bit of confusion here because there's a lot of fractions within fractions unfortunately, but what happens is that we're going to end up with a 24 on top because we multiply this by 24 over 24 and the 24 on the bottom will cancel with this 24 here. So we're left with 24 on the top, divided by 18 over density of gold, plus five over density of silver, plus one over density of copper. So we have 24 over 18 over 19.32 grams per cubic centimeter, that's the density of gold, then we have to look up the density of silver as well, five divided by 10.1 grams per cubic centimeter, plus one over the density of copper of 8.8 grams per cubic centimeter. This gives 15.6 grams per cubic centimeter is the density of the mixture called 18 karat gold.