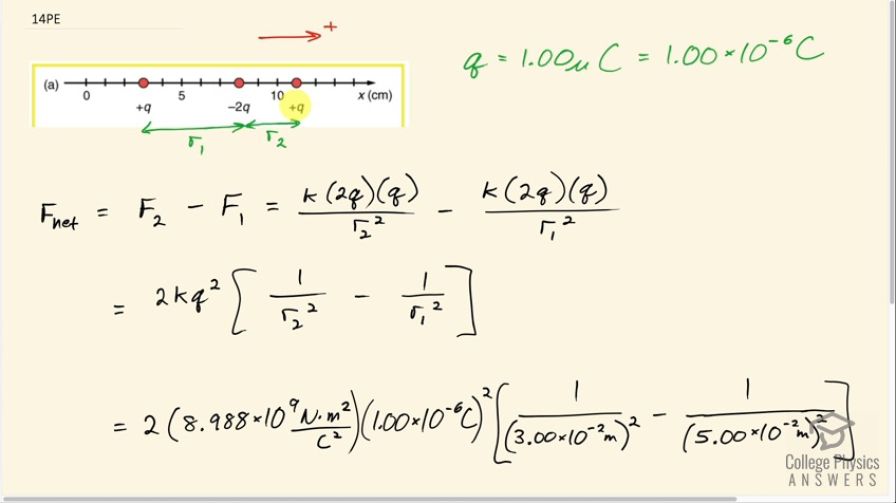
Question
What is the force on the charge located at in Figure 18.51(a) given that ?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 18, Problem 14 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This negative 2 times q charge in the middle will experience an attraction to this charge positive q to the right and then it will also experience an attraction to this positive q charge on its left but it's closer to the one on the right than it is to the left and they have equal magnitudes positive q and so there's gonna be a net force to the right; we are gonna take the right to be the positive direction. We are told that q is a charge of 1.00 microcoulombs which is 1.00 times 10 to the minus 6 coulombs and when we are doing our net force calculation here, we are going to ignore the sign of the charge here; we are going to just use magnitudes and the sign is something that we'll just introduce based on our understanding of what direction the force is in. So the force number 2, which we'll call the force on this center charge due to the right-hand charge, so this is F 2 in this direction— that's positive because it's to the right— and this force F 1 which is the force of attraction to the charge on this left side, we are gonna call that negative because it's directed towards the left and so the net force will be the right-hand force minus the left-hand force using magnitudes for all the charges. So the F 2 is going to be the Coulomb's constant times the first charge of magnitude 2q multiplied by the second charge of magnitude q divided by this distance r 2 between these two charges squared and then subtract from that the force of attraction to the left-hand charge which is k2q times q over r 1 squared. So this k, this 2 and the q squared can be factored out from both these terms and so we have 2kq squared times 1 over r 2 squared minus 1 over r 1 squared. So we have 2 times Coulomb's constant— 8.988 times 10 to the 9 newton meters squared per Coulomb squared— times 1.00 microcoulomb squared times 1 over 3.00 centimeters squared but I write centimeters as times 10 to the minus 2 meters because we can count the number of tick marks from the center charge to the right-hand charge and beginning here it's one tick-mark, two and three and we know that that's 3.00 centimeters because of this label here on this x-axis and then minus 1 over 5.00 times 10 to the minus 2 meters squared because there's one, two, three, four, five centimeters separating these charges and we end up with 12.8 newtons and this is positive meaning it is towards the right.
