Question
Assume that the turbines at a coal-powered power plant were upgraded, resulting in an improvement in efficiency of 3.32%. Assume that prior to the upgrade the power station had an efficiency of 36% and that the heat transfer into the engine in one day is still the same at . (a) How much more electrical energy is produced due to the upgrade? (b) How much less heat transfer occurs to the environment due to the upgrade?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 15, Problem 26 (Problems & Exercises)
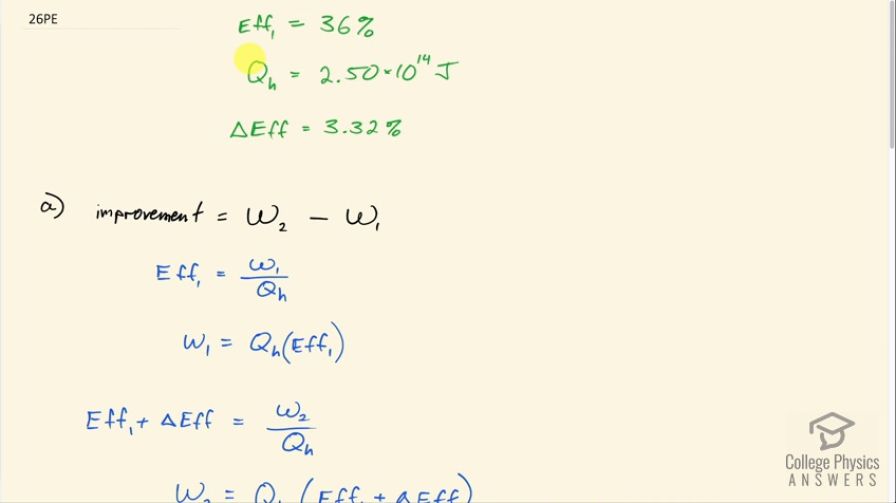
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A coal-fired power plant has a 36.0 percent efficiency originally so that's efficiency number 1; it absorbs some amount heat of 2.50 times 10 to the 14 joules and its efficiency is approved by 3.32 percent. So question (a) asks what is the improvement in electrical energy produced? We usually use w to represent the work done or the useful amount of energy created in a process. So efficiency 1 then is the work done in the first case, which is the amount of electrical energy produced, divided by the amount of heat absorbed to produce it. So the improvement is the work done in the second case after the improvement in efficiency minus the work done in the first case. So the work done in the first case then if we solve for it is by multiplying both sides by Q h is Q h times Eff 1. Now the second case, the efficiency will now be the original efficiency plus this improvement so that's the 36 plus 3.32 in other words and that equals the amount of electrical energy produced in the second case divided by the same amount of heat absorbed. So the Q h does not need a subscript 2 nor 1 because we are told it absorbs the same amount of heat in both cases. So w 2, after multiplying both sides by Q h, is Q h times Eff 1 plus ΔEff. So the improvement then is this w 2 copied here minus the w 1 which is copied here and distributing the Q h into the brackets makes Q h times Eff 1 plus Q h times ΔEff minus Q h times Eff 1. Well these make zero and so the improvement is the heat absorbed multiplied by the improvement in efficiency. So that's 2.50 times 10 to the 14 joules times 3.32 percent percent expressed as a decimal by dividing by 100 and that's 8.3 times 10 to the 12 joules. So the change in the amount of waste heat is this difference in heat sent to the cold temperature reservoir. So the change in the waste is going to be Q c 2 minus Q c 1. Well the work done in the second case— as it is for any cyclical engine— is the heat absorbed minus the heat expelled to the environment so in the second case, it's Q h minus Q c 2. We can solve for Q c 2 by adding it to both sides then subtracting w 2 from both sides. We get Q c 2 equals Q h minus w 2 and by the same logic, we can say Q c 1 equals Q h minus w 1. So then we substitute in place of Q c in this Δwaste formula here and we do that here and we have Q h minus w 2 which is a substitution for Q c 2 minus Q h minus w 1, which is a substitution for Q c 1 and then get rid of the brackets here and we have Q h minus w 2 minus Q h plus w 1— this minus and this minus here made a plus by the way— and we end up with w 1 minus w 2. While in part (a), we were calculating w 2 minus w 1 so this is the opposite of what we had in part (a) so the negative of w 2 minus w 1 so in other words, it's negative 8.3 times 10 to the 12 joules; this negative says that the amount of waste has been reduced.
