Question
(a) If you toss 10 coins, what percent of the time will you get the three most likely macrostates (6 heads and 4 tails, 5 heads and 5 tails, 4 heads and 6 tails)? (b) You can realistically toss 10 coins and count the number of heads and tails about twice a minute. At that rate, how long will it take on average to get either 10 heads and 0 tails or 0 heads and 10 tails?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 15, Problem 62 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
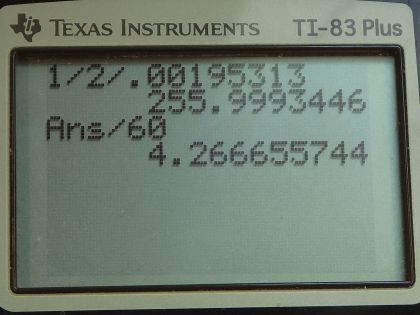
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When tossing 10 coins, what's the probability of getting six heads and four tails or five heads and five tails or four heads and six tails? So we need to take the total number of microstates of these three macrostates and divide that by the total number of possible microstates for any coin toss which is 1024. So we have 210 ways to make 6 heads and 4 tails, 252 ways to make 5 heads and 5 tails and 210 ways to make 4 heads and 6 tails; and that's 672 total microstates to make our desired condition here. So the probability is 672 divided by 1024 which is 65.6 percent. And part (b) asks supposing you can toss ten coins and count the number of heads and tails twice a minute, how long will it take to get 10 heads and 0 tails or 0 heads and 10 tails. So total number of microstates is 1 plus 1 which is 2 and so the probability is 2 divided by the total number of possible microstates which is 1024 and that's 0.00195313. And I give this some units, this is... you get this many desired states per throw because this is the desired states and this is total number of states... you know, each representing... you get 2 out of 1024 throws is another way to look at it so 2 desired states out of 1024 attempts. Okay! So the time then is gonna be 1 minute for every 2 throws multiplied by 1 throw for every this many desired states. And so we have 256.00 minutes per win you could say, or per desired state, meaning you get one of these two conditions here which in hours is 4.27 hours.