Question
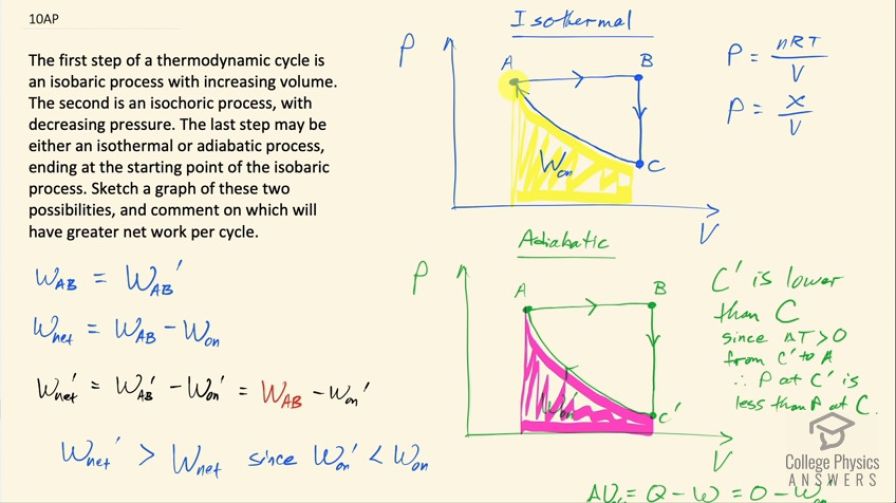
The first step of a thermodynamic cycle is an isobaric process with increasing volume. The second is an isochoric process, with decreasing pressure. The last step may be either an isothermal or adiabatic process, ending at the starting point of the isobaric process. Sketch a graph of these two possibilities, and comment on which will have greater net work per cycle.
Final Answer
The cycle with an adiabatic process will do greater net work per cycle.
Solution video
OpenStax College Physics for AP® Courses, Chapter 15, Problem 10 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two different thermodynamic processes but they begin the same way at point A and proceed with an isobaric process in which case, the pressure is constant and the volume is increasing until point B after which there's an isochoric process with a constant volume and a decreasing pressure and then from point C to point A in this top picture, we have an isothermal process and this curve follows the typical reciprocal curve of y equals 1 over x because this pressure is number of moles times the gas constant times temperature over volume but since temperature is constant in an isothermal process, this numerator is some constant number x say and it's divided by this changing V and so V is like... (well, I guess maybe I should have chosen the letter Z or something here) Z is like this constant and then V is like the x and P is like the y so it's of this form of a reciprocal graph so that's the curve here. And there's some work being done by the system from point A to B and then from point C back to A, there's work being done on the system and the work being done by the system is the same from point A to B in the isothermal as it is in the adiabatic process but there's a difference in the amount of work done on the system in the return from this point back to A and so the thing that distinguishes the adiabatic from the isothermal is the position of this point C after position B I call this C prime and C prime is lower down than point C is and we can see that if we overlay the two graphs. So the graphs are identical and they are really identical because I actually copied and pasted them but the amount of area shaded in pink is less than the amount of area shaded in yellow and so the net work done is going to be greater in the adiabatic process because there is less work done on the system to return it back to its initial state at point A. So we can say that over here so the work done from A to B is equal to the work done from A to B prime— I am using prime to denote anything happening in the adiabatic process— and the net work done is the work done from A to B minus the work done on the system and so that is this whole area here from A to B is work AB and then subtract from that the yellow-shaded area. And then we have the W net done in the adiabatic process is the work done from A to B, which is the same as the work done from A to B in the isothermal process and then subtract from that the work done on the system prime in this adiabatic case. So the net work done in the adiabatic case will be greater than the net work done in the isothermal case since the adiabatic case is subtracting away less work done on the system versus what's being subtracted away in the isothermal case. So I guess we could talk about why is this point C prime lower than point C? In other words, why is the area from C prime to A less than the area from C to A? And now because this is an adiabatic process, there's going to be a temperature change going from C prime to A the temperature will increase and we know that because the change in internal energy from C prime to A is Q minus W and since there's no heat transfer at all because it's adiabatic that means Q is 0 and so we have negative work done on the system from C prime to A is the change in internal energy and this work done on the system is less than zero because this term is meant to be their work done by the system and so the minus from the formula presumes that W is work done by the system but since work is being done on the system that makes this W negative and so we have minus a negative, which will make a positive change in the internal energy and the internal energy is related to the temperature and so I mean U is 3 over 2 times the number of atoms in an ideal monoatomic gas times Boltzmann's constant times temperature so if you have a positive change in internal energy, you can have a positive change in temperature. Okay! So this position's C prime is lower than C because with a decrease in volume causing an increase in pressure and an increase in temperature additionally causing an increase in pressure to get to the same pressure as before, we need to start at a lower pressure to begin with because there are these two contributions to increasing the pressure along this path and because pressure is nRT over V so we have a ΔT that's positive and a ΔV that's negative and so the ΔV is the same in the isothermal versus the adiabatic case but now we are throwing in a positive ΔT in the adiabatic case in which case, we need to begin at a lower pressure to end up at the same pressure in both scenarios. Okay! Well, hopefully some of that made sense and yes, we get more W net done in the adiabatic case.