Question
(a) A cyclical heat engine, operating between temperatures of and produces 4.00 MJ of work on a heat transfer of 5.00 MJ into the engine. How much heat transfer occurs to the environment? (b) What is unreasonable about the engine? (c) Which premise is unreasonable?
Final Answer
- The efficiency of 0.80 is greater than the Carnot efficiency of 0.41. This is not possible.
- Either less work was done, or more heat was input.
Solution video
OpenStax College Physics, Chapter 15, Problem 17 (Problems & Exercises)
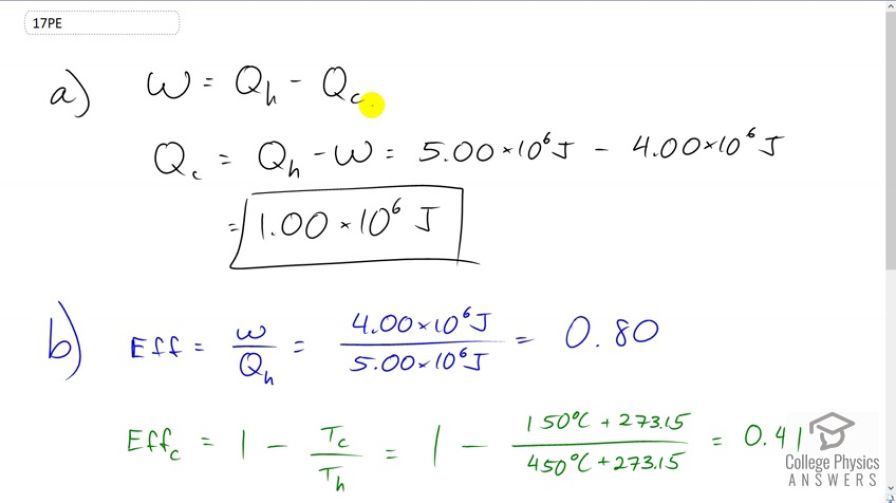
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Since we are dealing with a cyclical heat engine, we can say that the work done by it equals the energy it absorbs minus the energy lost to the cold temperature reservoir and we can solve for Qc by adding it to both sides and then also subtracting W from both sides. And then we end up with the energy lost to the environment is the energy absorbed minus the work done. So it's 5 times 10 to the 6 Joules of energy [unclear] whole minus 4 times 10 to the 6 Joules of work done, which is 1 point 00 times 10 to the 6 Joules of energy lost to the environment. Now we can tell what’s unreasonable about this engine by calculating its efficiency and comparing with the Carnot efficiency, which is the maximum theoretical possible efficiency. So the efficiency is the work done by it divided by the energy it absorbs. So that's 4 times 10 to the 6 Joules of work done then divided by 5 times 10 to the 6 Joules of energy absorbed which is 0.8 efficiency and the best theoretical efficiency you can possibly get is 1 minus the cold reservoir temperature divided by the hot reservoir temperature and expressed in Kelvins. So that's 1 minus 150 degrees Celsius plus 273.15 to convert to Kelvin, divided by 450 degree Celsius converted to Kelvin and that is 0.41 so the problem here is that the efficiency of 0.8 is greater than the maximum possible efficiency and so that's not possible. And so either less work was done in reality or more heat was input than is reported here.
