OpenStax College Physics, Chapter 15, Problem 52 (Problems & Exercises)

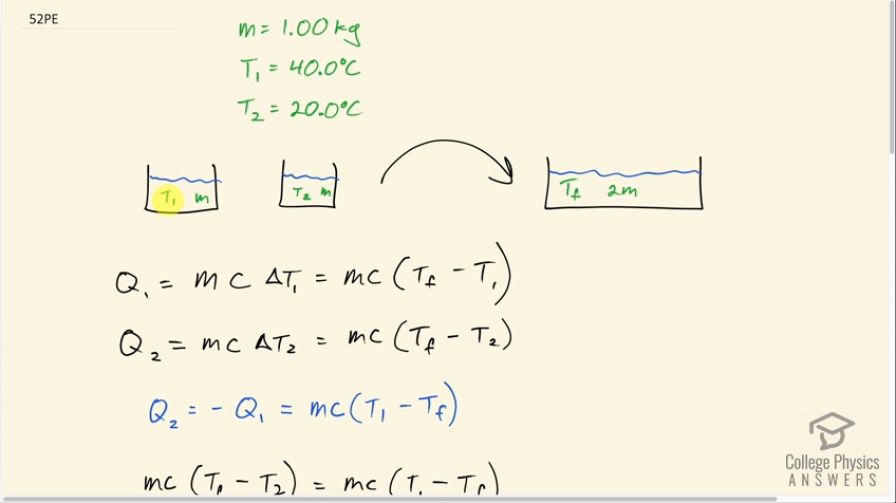
This is College Physics Answers with Shaun Dychko. Equal masses of water are going to be mixed together and the first sample of water has a temperature of 40.0 degrees Celsius and the second sample of water has a temperature of 20.0 degrees Celsius and each have a mass of 1.00 kilogram and there's no need to put an m 1 or m 2 subscript on these masses because they are the same so there's no need to distinguish them so we'll just call it m. They are going to reach some final temperature once they mix together in a mass of 2m. So the heat transferred out of sample 1 is gonna be its mass times its specific heat of water times the change in temperature for sample 1 which will be the final temperature minus the initial temperature and the heat transferred into sample 2 is gonna be mcΔT 2 and ΔT 2 is T f minus T 2. Now the heat transfer for the second sample is gonna be the negative of the heat transfer of the first sample this is to say that the first sample will be losing the same amount of heat that the second sample would be gaining and so their magnitudes will be the same and they will be the same if we put this negative in front of Q 1 and that essentially just turns around these two terms in this bracket so the T 1 becomes positive and the T f becomes minus when you put this negative in front of this. So that means we can equate this Q 2 with the negative of Q 1 and the negative of Q 1 is this and so write that here. So mc (T f minus T 2) equals mc (T 1 minus T f) and the mc's cancel on both sides and you are left with T f minus T 2 equals T 1 minus T f and then add T f to both sides and you get 2T f on the left and add T 2 to both sides and you get T 1 plus T 2 on the right then divide both sides by 2 and you get T f is T 1 plus T 2 all over 2. So turns out that because both samples are the same mass and the same specific heat, the final temperature will just be the arithmetic average of their initial temperatures. So that's 40.0 plus 20.0 all over 2 which is 30.0 degrees Celsius. So the heat transfer then into Q 2 from Q 1—from sample 1— is mc times (T f minus T 2). So that's 1.00 kilogram times 4186 joules per kilogram per Celsius degree times 30.0 degrees Celsius— final temperature— minus 20.0 degrees Celsius— initial temperature— and that's 4.19 times 10 to the 4 joules. Part (b) asks us for the total change in entropy. So that will be the sum of the entropy changes of the sample one and sample two. So for sample one, we have Q 1 divided by the average temperature of sample one and for sample two, the change in entropy will be the heat transferred into sample two divided by sample two's average number and these temperature's have to be in Kelvin by the way whenever you are dealing with changes in entropy. So the average temperature for sample one is its initial temperature— 40.0 degrees Celsius— plus 273.15 to convert into Kelvin plus 30.0 degrees Celsius plus 273.15 all divided by 2 which is 308.15 Kelvin and the average temperature of sample two is the average of 20.0 and 30.0 degrees Celsius both converted into Kelvin divided by 2 and that's 298.15 Kelvin. So the change in entropy then is Q 1 which is the negative of Q 2 and we said that up here... you know, you could multiply both sides by negative 1 here and you could say negative Q 2 is Q 1. So Q 1 is the negative of Q 2, we found Q 2 and so we write this number but with a negative sign in front in place of Q 1. So we have negative 41860 joules divided by the average temperature for sample one—308.15 Kelvin— plus the same heat transfer but not positive 41860 joules per Kelvin—heat going into sample two— divided by its average absolute temperature which is 298.15 Kelvin and this works out to a net increase in entropy of 4.56 joules per Kelvin.