Question
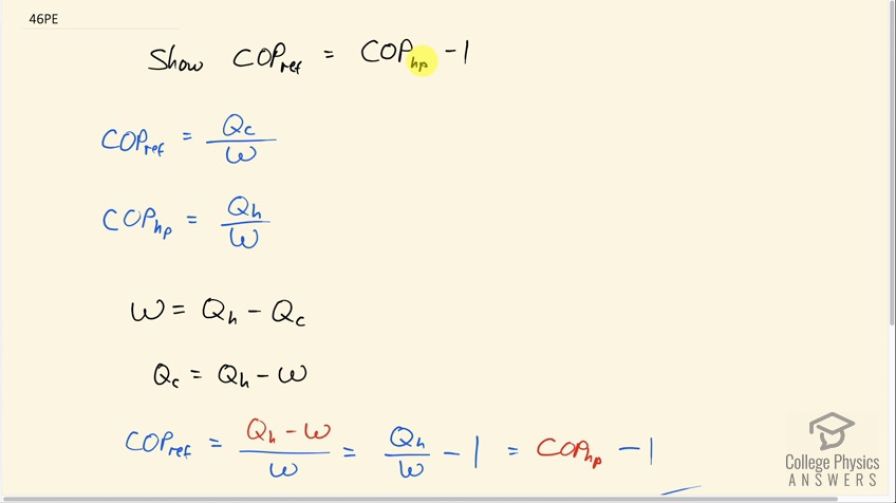
Show that the coefficients of performance of refrigerators and heat pumps are related by .
Start with the definitions of the 's and the conservation of energy relationship between , , and .
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 15, Problem 46 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to show that the coefficient of performance for a refrigerator is 1 less than the coefficient of performance for a heat pump. So the coefficient of performance for a refrigerator is the amount of heat that it takes out of the cold environment divided by the amount of work energy it takes to do that transfer and the coefficient of performance for a heat pump is the amount of heat delivered to the high temperature environment divided by the work it takes to do that. Now the conservation of energy relationship is that work is the heat transferred to the higher temperature environment minus the heat taken out of the cold temperature environment and we can rearrange this to solve for Q c so we'll add Q c to both sides and subtract w from both sides and we get Q c equals Q h minus w. And then make a substitution for Q c in our coefficient of performance for refrigerator formula so instead of Q c, we write Q h minus w there. And then we'll divide both of the terms in the numerator by this w and we end up with Q h over w minus 1 But Q h over w is the coefficient of performance for a heat pump and so we have shown what we needed to show. Coefficient of performance for a refrigerator is 1 less than the coefficient of performance for a heat pump.