Question
(a) What is the hot reservoir temperature of a Carnot engine that has an efficiency of 42.0% and a cold reservoir temperature of ? (b) What must the hot reservoir temperature be for a real heat engine that achieves 0.700 of the maximum efficiency, but still has an efficiency of 42.0% (and a cold reservoir at )? (c) Does your answer imply practical limits to the efficiency of car gasoline engines?
Final Answer
Solution video
OpenStax College Physics, Chapter 15, Problem 30 (Problems & Exercises)
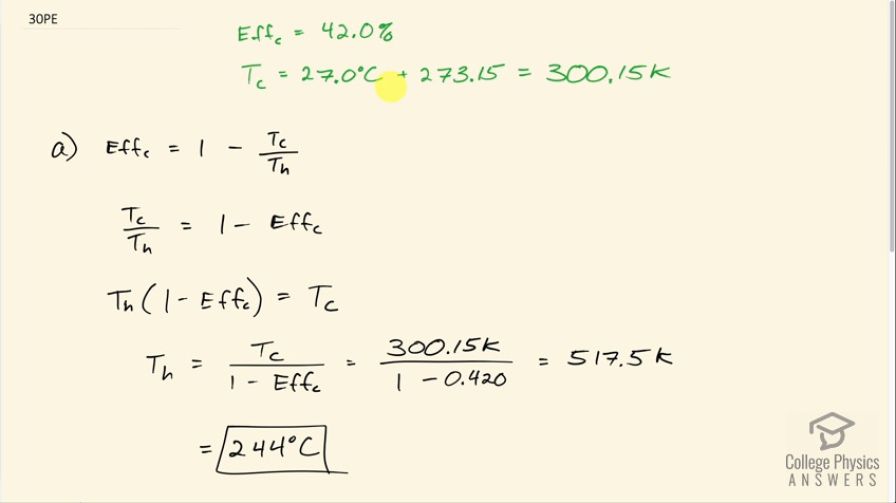
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A Carnot engine with an efficiency of 42.0 percent has a cold temperature reservoir at 27.0 degrees Celsius which is 300.15 Kelvin and our job is to find the temperature of the high temperature reservoir. So Carnot efficiency is 1 minus the T c divided by the T h and both of these have to be in Kelvin. And so I'm gonna add T c over T h to both sides and then subtract Eff c from both sides— and we are solving for T h here by the way— so this Carnot efficiency makes zero on the left leaving us with T c over T h on the left and on the right hand side, we are left with 1 minus Eff c. Then we'll multiply both sides by the high temperature and we get that T h times 1 minus Eff c equals T c and then divide both sides by 1 minus the Eff c. And we are left with the high temperature reservoir is the cold temperature reservoir divided by 1 minus the Eff c. So that's 300.15 Kelvin divided by 1 minus 0.420 which is 517.5 Kelvin and since the question gave us temperatures in degrees Celsius, we'll convert to degrees Celsius as well. So the high temperature reservoir in part (a) here is at temperature 244 degrees Celsius. In part (b), it tells us that there's a real engine that has an efficiency of 0.420, or 42 percent, and that engine is at 0.700 times the maximum possible efficiency; the maximum possible efficiency is another name for the Carnot efficiency. So that means 0.700 times the Eff c is 0.420 and then we can divide both sides by 0.700 to solve for what this hypothetical maximum efficiency would be so 0.420 divided by 0.700 is 0.600. And then we can use this same formula that we derived up here for the high temperature reservoir in terms of the cold temperature and the Carnot efficiency to figure out what the high temperature would be. So it says in the question that the cold reservoir is still at 27.0 degrees Celsius which is 300.15 Kelvin and we divide that by 1 minus 0.600 and that gives 477 degrees Celsius.


