OpenStax College Physics, Chapter 15, Problem 60 (Problems & Exercises)

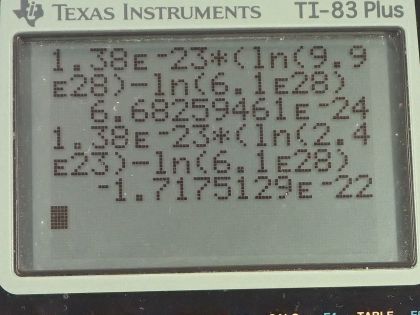
This is College Physics Answers with Shaun Dychko. We are going to find the total change in entropy if you start with 45 heads and 55 tails among 100 coins and flip them and end up with 51 heads and 49 tails. So the change in entropy will be the final amount of entropy minus the initial amount of entropy and the entropy in each case is Boltzmann's constant multiplied by the natural logarithm of the number of microstates that make up this state. So we can factor out k by the way so we have k times ln of w f minus ln of w i. So the number of microstates for 51 heads and 49 tails we can look up in table [15.4] and that is 9.9 times 10 to the 28 and then we take the natural logarithm of that and subtract from that the natural logarithm of the number of microstates in which we have 45 heads and 55 tails so 45 heads and 55 tails is 6.1 times 10 to the 28 microstates. Multiply that difference by the Boltzmann's constant— 1.38 times 10 to the minus 23 joules per Kelvin— and we get 6.68 times 10 to the minus 24 joules per Kelvin is the total change in entropy so it increases by a very very small amount. In part (b), what if we get 75 heads and 25 tails in the end? So that changes w f so now we have 75 heads and 25 tails which is 2.4 times 10 to the 23 microstates so w f is 2.4 times 10 to the 23 everything else is the same and we end up with negative 1.72 times 10 to the minus 22 joules per Kelvin. So the total entropy has decreased in this case because we have ended up with a less probable state than we started with. In part (c), we are gonna compare the probabilities of the scenario in (a) where we end with 51 heads and 49 tails versus (b) where we end with 75 heads and 25 tails and so we'll take the probability in scenario (a) so that will be the number of microstates that make up scenario (a) which is 9.9 times 10 to the 28 and divide that by the total number of all microstates and then we'll divide that by probability (b) but instead of dividing by this fraction, we are going to multiply by its reciprocal so I am multiplying by the reciprocal of the probability of (b) which is 1.27 times 10 to the 30 divided by 2.4 times 10 to the 23— this being the number of microstates for 75 heads and 25 tails. These cancel and so we take this ratio here and that is 4.13 times 10 to the 5. So 51 heads and 49 tails is more probable than 75 heads and 25 tails by a factor of 4.13 times 10 to the 5. Then in part (d), it asks does either outcome violate the second law of thermodynamics? No because the total entropy of the universe can still increase despite the local decrease in entropy that happens when we get 75 heads and 25 tails in scenario (b) and this could happen by the heat energy needed to flip the coins or some other process that increases entropy.