Question
Practical steam engines utilize steam, which is later exhausted at . (a) What is the maximum efficiency that such a heat engine can have? (b) Since steam is still quite hot, a second steam engine is sometimes operated using the exhaust of the first. What is the maximum efficiency of the second engine if its exhaust has a temperature of ? (c) What is the overall efficiency of the two engines? (d) Show that this is the same efficiency as a single Carnot engine operating between and . Explicitly show how you follow the steps in the Problem-Solving Strategies for Thermodynamics.
Final Answer
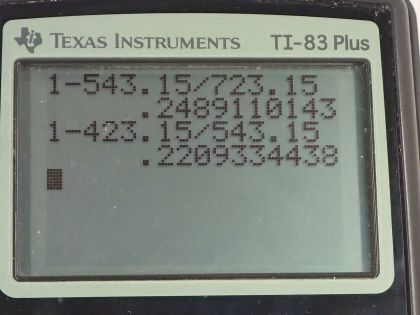
- 24.9%
- 22.1%
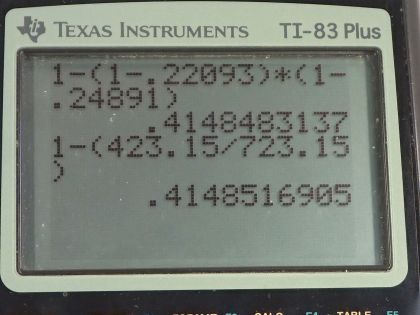
- 41.5%
- 41.5%
Solution video
OpenStax College Physics, Chapter 15, Problem 32 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A steam engine has steam at 450 degrees Celsius which is 723.15 Kelvin and it exhausts the steam at a temperature of 270 degrees Celsius which we convert into Kelvin and then we suppose that there's a second steam engine as well which exhausts steam at a temperature of 150 degrees Celsius and it uses this steam that's exhausted from the first engine as the input for the second engine. Now in part (a) we are asked... just consider one engine operating by itself, what is its maximum efficiency which is another name for Carnot efficiency? So Carnot efficiency is 1 minus the exhaust temperature divided by the incoming steam temperature. So that's 1 minus 543.15 Kelvin divided by 723.15 Kelvin which is 24.9 percent. Okay! And then part (b) asks what would the efficiency of the second engine be assuming that the input temperature for the second engine is the output temperature of the first engine? And so the Carnot efficiency of the second engine is 1 minus 423.15 Kelvin, which is 150 degrees Celsius converted into Kelvin, divided by the exhaust temperature of the first engine which is 543.15 Kelvin and that efficiency is 22.1 percent. Now in part (c), we are asked to figure out the total efficiency of these two engines operating together and that will be the total work done divided by the heat absorbed from the high temperature reservoir. So the total work done will be the work done by the first engine plus the work done by the second engine and the work for any cyclical engine can be written as the heat absorbed minus the heat exhausted. So for the first engine, it's Q h 1 minus Q c 1 and then for the second engine, it's gonna be Q h 2 minus Q c 2. But we are told that the heat absorbed by the second engine is the heat exhausted by the first engine. So we'll replace Q h 2 with Q c 1 in this w 2 formula. And then we'll make substitutions for the total work replacing w 1 with Q h 1 minus Q c 1 and then plus the Q c 1 minus Q c 2 in place of w 2 and then the Q c 1's make zero and we are left with Q h 1 minus Q c 2. And this makes sense; the total work done is the heat absorbed from the first high temperature reservoir minus the heat exhausted in the end by the second engine. So we can replace w T with this and then divide both terms on the top by Q h 1 and we have 1 minus Q c 2 divided by Q h 1 is the total efficiency. So we don't know what these Q's are though but we can rewrite them in terms of efficiencies that we do know. So the efficiency for the second engine is Q h 2 minus Q c 2 over Q h 2 but Q h 2—the heat absorbed by engine 2— is the heat exhausted by engine 1 so we'll replace Q h 2 with Q c 1 using this relation here. And then solve for Q c 1 first by multiplying both sides by it and then we are left with Q c 1 times Eff c 2 equals Q c 1 minus Q c 2 and then Q c 2 when you move it to the right hand side by adding it to both sides and then move this to the left hand side and then switch the sides around, you have Q c 2 equals Q c 1 minus Q c 1 times Eff c 2 and this Q c 1 can be factored out. So the heat exhausted by the second engine is the heat exhausted by the first engine as it turns out because this Q h 2 got replaced by Q c 1 times 1 minus the second engine's efficiency. So that gives us something to replace Q c 2 with in terms of efficiency; it still has this Q c 1 that we don't know but we'll see that by writing Q h 1 in terms of efficiency, this Q c 1 will end up canceling. So the efficiency of the first engine is Q h 1 minus Q c 1 over Q h 1 and we are gonna solve this for Q h 1 because we want to make a substitution for this. So times both sides by Q h 1 and then we have Q h 1 minus Q c 1 on one side equals Q h 1 times Eff c 1 on the other. And then bring this to the left side by subtracting it from both sides and bring this to the right side and we have Q h 1 minus Q h 1 times Eff c 1 equals Q c 1 and then factor out the Q h 1 and then divide both sides by 1 minus Eff c 1 and you have Q h 1 is Q c 1 divided by 1 minus Eff c 1. Okay! Now we are ready to make substitutions because we have Q h 1 in terms of efficiency and we have Q c 2 in terms of efficiency. So the total efficiency is 1 minus Q c 2 which is Q c 1 times 1 minus Eff c 2 divided by Q h 1 which is this fraction. Now dividing by a fraction is confusing so I like to multiply by the reciprocal instead so I'm multiplying by 1 minus Eff c 1 divided by Q c 1. We see that the Q c 1's fortunately cancel and we have 1 minus 1 minus the Eff c 2 times 1 minus Eff c 1— both of which we know. So 1 minus bracket 1 minus 0.22093 times 1 minus 0.24891 gives 41.5 percent efficiency. Now it turns out that we could have calculated that using the overall efficiency by talking about the temperature of the second engine's exhaust temperature and divide that by the temperature of the first engine's high temperature reservoir. So 1 minus 423.15 Kelvin—temperature of the exhaust from second engine— divided by 723.15 Kelvin—temperature of the high temperature reservoir of the first engine— and this also gives 41.5 percent.