Question
Find the magnitudes of velocities vAv_A and vBv_B in Figure 3.55.
<b>Figure 3.55</b>
Figure 3.55
Question by OpenStax is licensed under CC BY 4.0
Final Answer

vA=3.45 m/sv_A = 3.45 \textrm{ m/s}
vB=3.94 m/sv_B = 3.94 \textrm{ m/s}

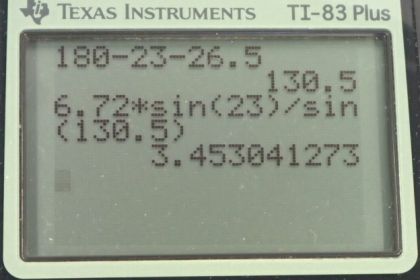
Solution video

OpenStax College Physics, Chapter 3, Problem 10 (Problems & Exercises)

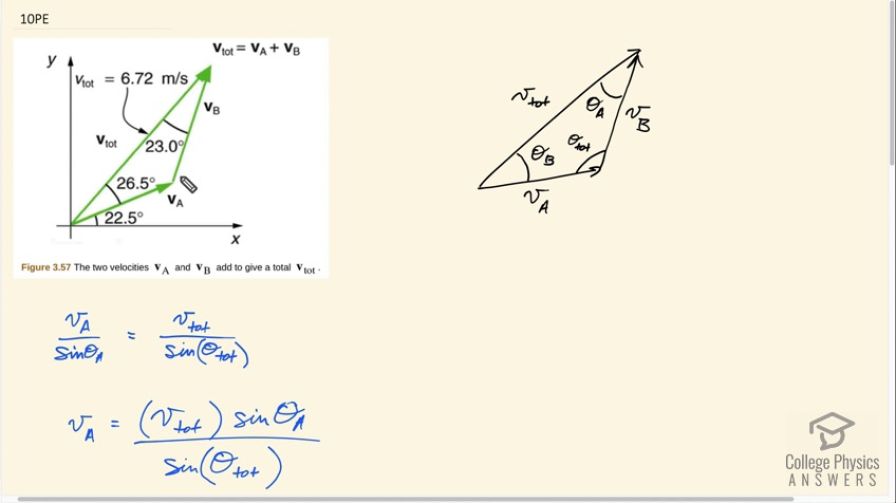
OpenStax College Physics, Chapter 3, Problem 10 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 3, Problem 10 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 3, Problem 10 (PE) calculator screenshot 2
Video Transcript
This is College Physics Answers with Shaun Dychko. Our job was to figure out how long vector A is and how long vector B is in this picture. Now, the sine law is what's going to do this for us the most efficient way. The sine law says that when you take a side length and divide it by the opposite angle, so consider this side length V A and divide by sine of the opposite angle, which is 23 degrees here, that's going to equal any other side length divided by the sine of its opposite angle. We have the side length V total, divided by its opposite angle, which we can figure out because we know two of the interior angles of this triangle. We can take 180 minus the sum of these two to get this angle here. We can solve for V A by multiplying both sides by the sine of theta A. Then we have V A is V total times sine theta V divided by sine theta of the total. I'll label this theta total because it's the angle opposite V total. Theta total is 180 minus the other two angles, and that's 180 minus 23 minus 26 and a half, which is 130.5. The length of V A then is the length of the total which is 6.72 meters per second. Multiply by sine of 23, which is 23 being the angle opposite VA, and divided by sine 130.5 for length of 3.45 meters per second. The same fancy trick can be used for finding the length of V B as well. We can say V B divided by the sine of the angle opposite this side which is here, theta B equals V total over sine theta total. Then we solve for V B by multiplying both sides by sine theta B. We get V B equals 6.72 times sine 26 and a half degrees divided by sine 130.5 degrees, iving a length of 3.94 meters per second.

Comments

Could you help me find which part of chapter 3 this formula is found? Thanks!

I just got this problem wrong on my assignment when I used your answers

Hi rickylove, the answer here is correct so far as I can tell but if there's a point in the video where you think there's an error, please mention the time when you think that is. Using the sine law might be an unfamiliar problem solving approach. Each student needs to choose the method that works for them.
All the best,
Shaun

Hi Shaun,

Can we solve for Vb once Va is discover by just subtracting Va from V total. If so shouldn't the answer for the equation be Vb = 3.27? Thank you in advance.

I just want to mention that this worked for my problems when I used this method. So it does seem to be correct as far as I can tell here.

Is there an alternate way to solve this without the sine law?

Hi torihall,
Thank you for the question. Yes, it's possible to solve this without the sine law. One alternative approach would be to use components: create an equation for each axis, where the x-component of the resultant equals the sum of the x-component of vectors A and B, and likewise for the y-axis. You would need to calculate the angle of vector B with respect to the horizontal first, based on the information in the picture. This creates two simultaneous equations which can be solved, probably by the method of substitution where you solve one of them for vector A in terms of vector B and v_tot, and substitute that into the other equation. The algebra gets a bit messy, so my preference is for the sine law approach, but the component method is good practice too.
I know this is a bit abstract, but hopefully it can help you start your own solution with this method,
Shaun

Hi, thanks for these videos, I was just wondering if you could explain why you used the angle of 23 degrees for angle A. how do you determine which angles are which. Im just a bit confused by that. Thanks !

Hello, are you asking why each angle gets labeled with their particular letters? Angle A is the corner opposite the side labeled with "A". Opposite means, with your pencil on a side (such as vAv_\textrm{A}), if you move your pencil through the triangle to the corner that is not at either end of the side, that's the opposite angle.
Hope this helps,
Shaun

I see that the sine law is the one that works best, but could you explain how you determined the sine law is the one you should use for this problem? thanks!

Using the sine law is just personal preference. To me, it's less effort than to use components. The component method in this case would mean creating two simultaneous equations, one for each dimension, then solving for the two unknowns vAv_\textrm{A} and vBv_\textrm{B}...

Hi Dieter, thank you for the question. Since VaV_\textrm{a} and VbV_\textrm{b} form two sides of a triangle with VtotV_\textrm{tot}, we expect the numerical lengths of VaV_\textrm{a} and VbV_\textrm{b} to have a total that is greater than the length of VtotV_\textrm{tot}. The shortest distance between two points, which in this case is the origin and the top of VbV_\textrm{b} or VtotV_\textrm{tot}, is a single straight line connecting them. VtotV_\textrm{tot} is that single shortest straight line. The alternative path along first VaV_\textrm{a}, then VbV_\textrm{b} will be longer.

Hope this helps,
Shaun