Question

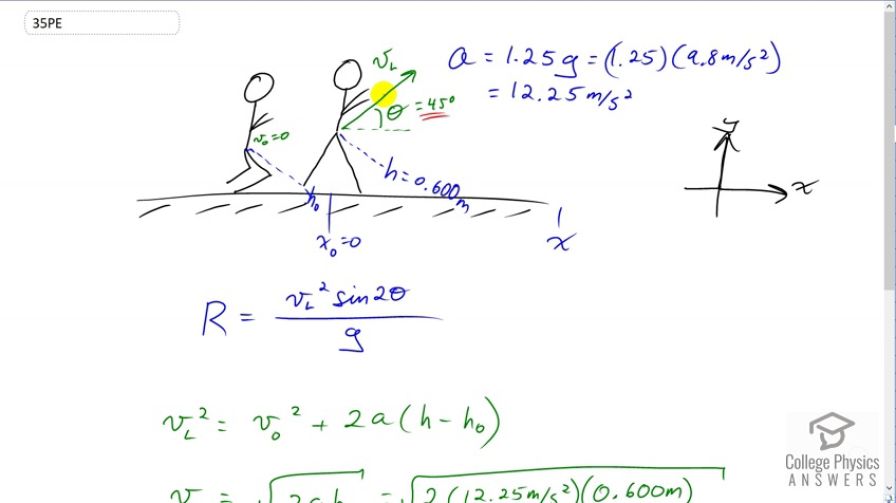
In the standing broad jump, one squats and then pushes off with the legs to see how far one can jump. Suppose the extension of the legs from the crouch position is 0.600 m and the acceleration achieved from this position is 1.25 times the acceleration due to gravity, gg . How far can they jump? State your assumptions. (Increased range can be achieved by swinging the arms in the direction of the jump.)

Question by OpenStax is licensed under CC BY 4.0
Final Answer

1.50 m1.50 \textrm{ m}

Solution video

OpenStax College Physics, Chapter 3, Problem 35 (Problems & Exercises)

OpenStax College Physics, Chapter 3, Problem 35 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 3, Problem 35 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We're told that this long-jumper is crouched 0.6 meters down and then they're going to extend their legs and launch themselves into this long jump. They're going to have acceleration while they extend their legs of 1.25 times g. So that's 1.25 times 9.8 which is 12.25 meters per second squared. We're asked to find out how far will they go. Now this picture is meant to show the long-jumper at two different times. This guy is meant to be in the same place as this guy. It's the same person but just at two different times. This is drawn here after the legs are extended. So, we're going to take this to be the position zero, and then they land over here somewhere, and they're going to land at the same height as they started with, so that means we can use this range formula. That is a very convenient formula, makes our work much easier. Now we're not given the angle of launch though. We can figure out what the launch velocity is based on this acceleration and knowing that it occurs over a distance of 0.6 meters. But we don't know what the angle is and we're told to make some assumptions in the question. So our assumption will be that this long-jumper will choose an angle that optimizes the range. They'll choose an angle such that the range is the greatest. Assuming no air friction, which is what we are always assuming in questions in the text book, the angle for the greatest range is 45 degrees because the sine of something can at most be one. You can never sine of anything being greater than one. So, what angle here makes a sine of one? Well the sine of 90 is one and so whatever angle makes this thing here into 90 is what will work. So we want to make that 2theta equal to 90 and we can do that by dividing both sides by two and we can see that theta is 45.So that's our assumption. The long-jumper is aware of physics and they will launch themselves at 45 degrees. Okay. So now the problem is then to figure out what this launch velocity is. So we know that the launch velocity squared is going to be the initial velocity here squared which is zero because this is a long-jumper, they start from rest, plus two times the acceleration which we are given, times the distance over which this acceleration occurs, the extension of the legs, h minus h naught, h naught being zero. So this simplifies to this line here and then we'll take the square root of both sides to get the launch velocity. The launch velocity is square root of two, times acceleration of 12.25 meters per second squared, times the extension of the legs, 0.6 meters, and that gives 3.8341 meters per second. Keeping lots of digits there because this is an intermediate calculation. Now the range is going to be that launch velocity squared, multiplied by the sine of 90 which is one, divided by 9.8, giving us a range of 1.50 meters.

Comments

do you solve this by assuming the initial velocity is the velocity you leave the floor with at the start of your jump? I assume this because this is the only way to solve the problem, however I had a thought that the jumper has no velocity at the start, but since were solving for how far he can jump, we would assume that initial velocity would be when he is leaving the floor and final velocity would be zero ( when he lands his jump)

Hi hms, yes, there is an initial velocity when the jumper's shoes leave the ground and they are finished accelerating. There is a similar misunderstanding here as in your previous question here where it's important to apply the formulas only while acceleration is constant. In this case there are two relevant periods of constant acceleration: 1) when the jumper is pushing off the ground with their legs, and 2) when they are moving through the air with constant acceleration due to gravity. Your question suggests a third period when they are pushed again by the ground to rest when landing, but this isn't relevant since our analysis will end the instant before hitting the ground. We don't know how hard the ground pushes on them when landing, and even if we did it doesn't have an affect on their range.

The problem solving approach seeks to calculate the final velocity after period 1). This feeds into the initial velocity of the range formula since the final velocity of period 1) is their launch velocity from the ground.

Hope this helps,
Shaun

How does your launch velocity = to your V0y. Why is that the case in this problem. Vo = Vosintheta, so wouldnt we set that up after we find the V0y?

Hi hms, thank you for the question. voyv_\textrm{oy} isn't part of this solution. Since we're using the range formula we want to know the magnitude of the launch velocity and plug that in for vLv_\textrm{L} and assume that is directed at 45∘45^\circ in order to maximize the range.
All the best,
Shaun