Question
Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements A⃗\vec{A} and B⃗\vec{B} , as in Figure 3.53, then this problem asks you to find their sum R⃗=A⃗+B⃗\vec{R} = \vec{A} + \vec{B} .)
<b>Figure 3.53</b>
Figure 3.53
Question by OpenStax is licensed under CC BY 4.0
Final Answer

30.8 m, 54.2∘ N of W30.8 \textrm{ m, } 54.2^\circ \textrm{ N of W}
It's a bit unclear how to interpret what the question means by "compass direction". According to Wikipedia, an "absolute bearing" on a compass is measured in the clockwise direction starting from North, in which case this answer would have an absolute bearing of 324.2∘324.2^\circ. Other systems of measuring with a compass require being specific about which cardinal direction one is measuring with respect to.

Solution video

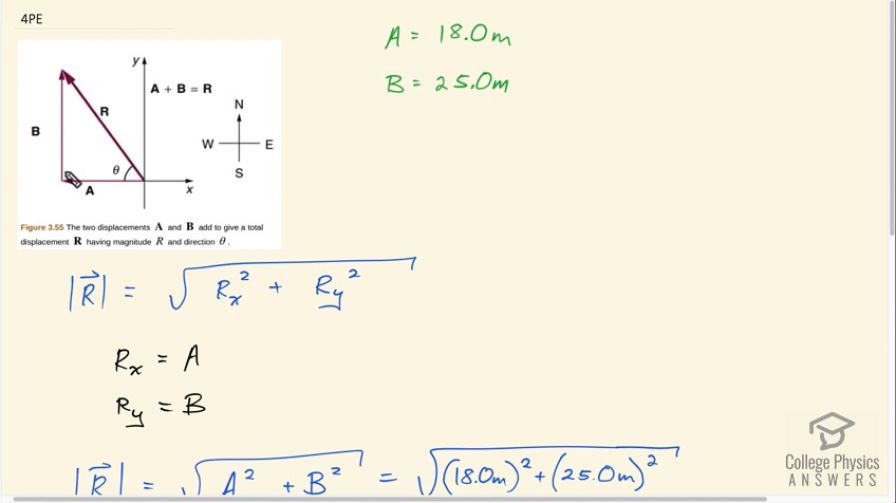
OpenStax College Physics, Chapter 3, Problem 4 (Problems & Exercises)

OpenStax College Physics, Chapter 3, Problem 4 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

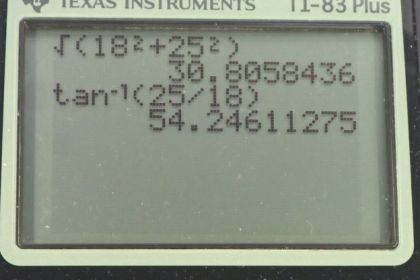
Calculator Screenshots

  • OpenStax College Physics, Chapter 3, Problem 4 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We imagined that we start at the origin and walk 18 blocks to the west and then 25 blocks to the north. This vector A has length 18 meters and vector B has length 25 meters. The question is, what is our displacement? This vector R is the resultant connecting our starting point to our ending point and we're going to find its length and its direction. The direction will express as theta, a certain number of degrees north of west. The length of this resultant is the length of hypotenuse because this is a right triangle conveniently, and so we can take the x and y components of this resultant, and they are going to be vectors A and B respectively. The length of this resultant vector is the square root of its x-component squared plus its y-component squared. Then we substitute in A and B for those components. We have the link for the resultant as a square root of the length of A-squared plus length of B-squared. That's the square root of 18 meters squared plus 25 meters squared, which gives the length of 30.8 meters. The angle theta, we can get by using inverse tangent because we know the opposite leg of this right triangle and the adjacent leg. We take the inverse tangent of the opposite length divided by the adjacent length. Its inverse tangent of 25 meters vertical divided by 18 meters horizontal, which is 54.2 degrees. That's this angle in here, which is towards the north compared to west, so north of west. Our final answer then for the resultant vector is that we are 30.8 meters from the starting point at an angle of 54.2 degrees north of west.

Comments

How is tan-1(25/18) 54.246? When I calculate it on my calculator it answers .94677. How do you change this answer to degrees

Hi tumbled129, this really depends on the brand of calculator you're using. Often there will be small "rad" or "deg" displayed if you look closely at your screen, and you'll have to either look up a manual for your calculator or use some trial and error button pushing to see how to change it. Alternatively, although this is inconvenient but it works, you could convert radians into degrees by multiplying by 180/3.14159. 0.94677 radians * 180 / 3.14159 = 54.246 degrees.
Good luck!
Shaun

The answer to the degrees is 35.75. 54.2 is wrong

Hi Joe, thank you for this comment. We're both right! :) It's important to be more specific about the position of the angle however. In the figure the angle theta is positioned North of West. The direction is 54.2∘ N of W54.2^\circ \textrm{ N of W}. Equally correct, but requiring explicit directions, is 35.8∘ W of N35.8^\circ \textrm{ W of N}. 35.8∘35.8^\circ is the complement to 54.2∘54.2^\circ.
All the best,
Shaun