Question
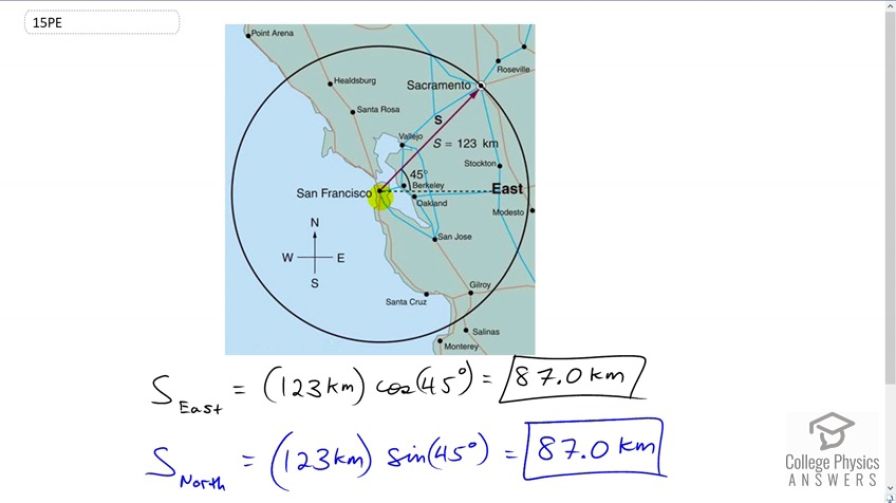
Find the north and east components of the displacement from San Francisco to Sacramento shown in Figure 3.57.
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 15 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the x and y components of the displacement between San Francisco and Sacramento. So the component to the east is the x component and that's along here. Then the component north is the y component which we'll draw in blue [inaudible 00:22]. So this is sector S subscript y or I read it actually as S subscript north. Across here horizontally we have S subscript x or I write it as S subscript east. So the easterly component is the length of the hypotenuse which is 123 kilometers multiplied by cosine of 45 degrees and that gives 87.0 kilometers. We use cosine because the horizontal component is the adjacent leg of this right triangle. We find the adjacent leg of a right triangle always by multiplying the angle times -- the cosine of the angle by the hypotenuse length. Because this is a special triangle, 45 degrees, we know that the northerly component is also going to be the same amount, 87.0 kilometers. There is no need to plug this line in blue into the calculator because as a special triangle, it has these -- if we were to reduce it, it would have length of one and root two, each leg being of length one and the hypotenuse being root two times each of the legs. So cos 45 and sine 45 are the same. So cosine of 45 is one over root two and we'll see that if we took the sine of 45 being the opposite over the hypotenuse, it would be the same amount. So sine 45 is also one over root two. That's helpful to memorize these special triangles. This is one of them and then the other one is thirty degrees and sixty degrees and a right angle there and one, two and root three. From this triangle you can see that cosine of 60 is a half and the sine of 60 is root three over two and cosine of 30 is root three over two and the sine of 30 is one half. Anyway, so there we go.