Question
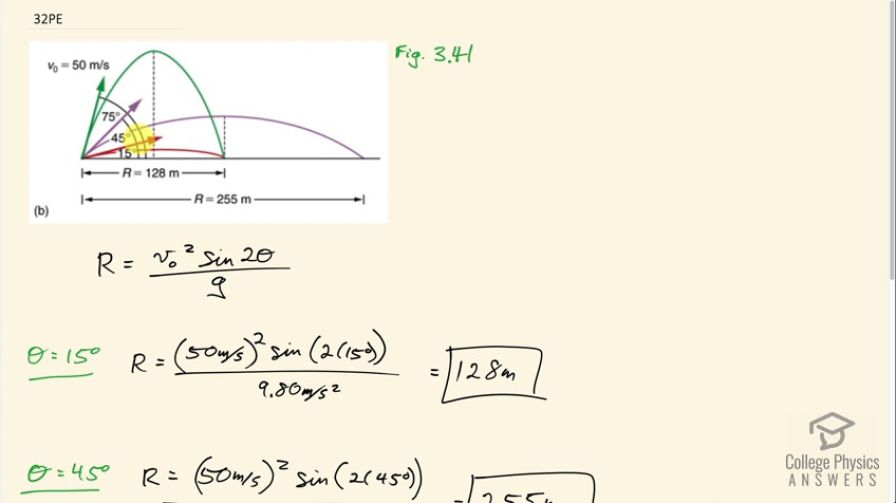
Verify the ranges shown for the projectiles in Figure 3.40(b) for an initial velocity of 50 m/s at the given initial angles.
<b>Figure 3.40</b> The range for a projectile which falls to its initial height is given for various launch angles, all with the same initial speed.
Figure 3.40 The range for a projectile which falls to its initial height is given for various launch angles, all with the same initial speed.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

Please see the solution video.

Solution video

OpenStax College Physics, Chapter 3, Problem 32 (Problems & Exercises)

OpenStax College Physics, Chapter 3, Problem 32 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 3, Problem 32 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 3, Problem 32 (PE) calculator screenshot 2
Video Transcript
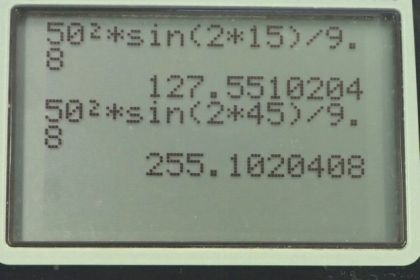
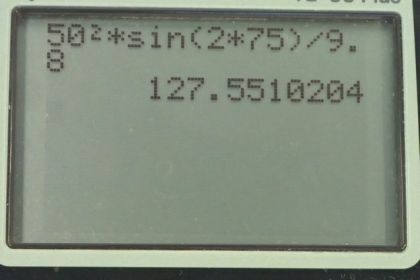
This is College Physics Answers with Shaun Dychko. In figure 3.41, we have three different launch angles for the same speed of 50 meters per second. And we're going to verify that the range or the horizontal displacement where the projectile lands from where it started, is going to be as shown on this picture. So for a 15 degree launch angle, we expect the range to be 128 meters. And likewise for a 75 degree launch angle, we expect the range to still be 128 meters. Whereas, for a launch angle of 45 degrees along this purple line, we expect a range of 255 meters. So we can calculate these distances using the range formula: which is equation 71 in chapter three; So the initial speed squared, multiplied by the sine of two times the launch angle, divided by the acceleration due to gravity is the range. So for 15 degrees, we have the range is 50 meters per second initial speed squared, times sine of two times 15 degrees, divided by 9.8 meters per second squared, which is 128 meters. And then for 45 degrees; we’re plugging-in 45 in place of 15, and otherwise the values are the same, and we get a range of 255 meters. And then for 75 degree launch angle, we have 50 meter per second squared, times sine of two times 75 degrees divided by 9.8, giving a 128 meters.