Question
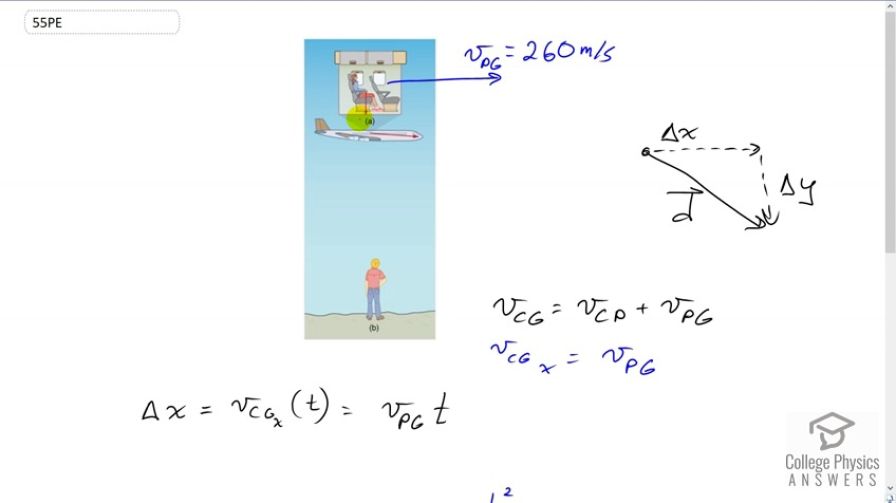
Verify that the coin dropped by the airline passenger in the Example 3.8 travels 144 m horizontally while falling 1.50 m in the frame of reference of the Earth.
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 55 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. As the passenger on this plane drops the coin, they perceived the coin go straight down, but a person on the ground will see the coin going down towards them and to the right where the component of the velocity of the coin with respect to the ground in the horizontal direction is going to be equal to that of the plane. Because the coin is not thrown forwards or backwards within the plane and so the x component of the coin’s velocity with respect to the ground is going to be the velocity of the plane. And so we’ll find the horizontal component of the coin’s displacement, by saying the x component of the velocity of the coin with respect to the ground multiply by the time it spends falling to the floor of the plane. This is equal to velocity of the plane with respect to the ground. And so our job first to figure out what this time is, and then we know that the final y position minus the initial y position of this coin is going to equal any initial velocity that it has which is none, plus one half times its vertical acceleration times time squared. We’ll solve this for t by multiplying both sides by two over ay. Switching the sides around and then taking the square root of both sides, and so the time is gonna be the square root of two times the vertical displacement divided by the vertical acceleration. So that’s two times y minus y naught over negative g. That’s square root of two times the final position which we’ll take to be zero, minus the initial position which we’ll say is positive 1.5 meters, divided by negative 9.8 meters per second squared. Square rooting all that gives us this amount of time it spends falling, just over half of a second. We’ll take that time multiply by 260 meters per second, speed of the plane, and that gives the horizontal displacement of the coin as seen by a earth-based observer as 144 meters.
