Question
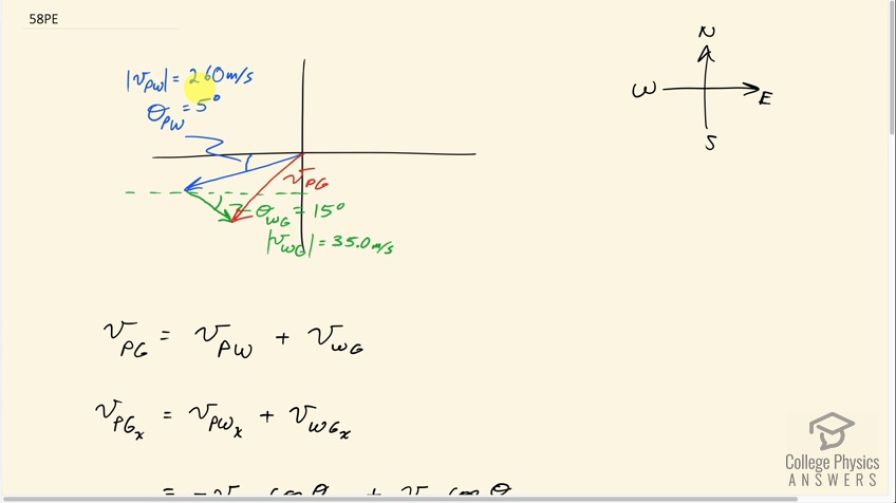
(a) A jet airplane flying from Darwin, Australia, has an air speed of 260 m/s in a direction south of west. It is in the jet stream, which is blowing at 35.0 m/s in a direction south of east. What is the velocity of the airplane relative to the Earth? (b) Discuss whether your answers are consistent with your expectations for the effect of the wind on the plane's path.
Final Answer
- The wind should deflect the plane further South. The angle S of W has increased, as expected.
Solution video
OpenStax College Physics, Chapter 3, Problem 58 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
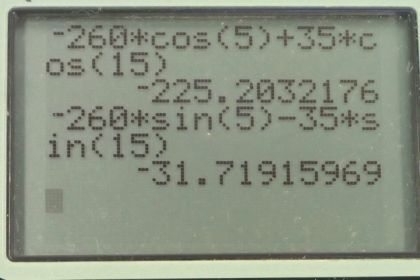
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This plane has a velocity with respect to the wind. So I have the subscript p for plane and w for wind. And it’s going at a speed of 260 meters per second, five degrees south of west. So that’s represented by this blue arrow and then we're told that the wind has its own velocity with respect to the ground. And so I have w for wind and g for ground here. And it’s going at a direction of 15 degrees south of east with a speed of 35 meters per second. Now when we're adding relative velocities, when we have the inner subscripts the same. Then we find that they cancel, and we're left with the velocity of the outer subscripts. So that is p and g. So that is velocity of the plane with respect to the ground. And that's what this question asks us to find. And, so to get this plane with respect to ground velocity; we have the velocity of the plane with respect to the wind, to the velocity of the wind with respect to the ground. And so that’s this red resultant line here, when we use the head to tail method of adding the blue and green vectors. So, we're going to figure out the x and y-components of this velocity of the plane with respect to the ground, by adding the components of the two other vectors together. So the x-component of the plane with respect to the ground, is the x-component of the plane with respect to the wind, plus the x-component of the wind with respect to the ground. And the plane is going to the leftish. And so we have a negative in front of its x-component. And if we were to draw the x-component, it would be a dotted line like this. So this is the velocity of the plane with respect to the wind, x-component. And it is the adjacent leg of this triangle here. Adjacent to this angle theta p w here. And we’ll use cosine of that angle multiplied by the length of a hypotenuse to get this x-component. And putting a negative in front of it, because it’s directed to the left. And the x-component of the wind with respect to the ground is going to be positive. Since it is to the right, here’s the x-component ends here. And it’s the adjacent leg is well. So we also use cosine of the wind with respect to the ground angle. And so we have 35 times cos 15, and then we have negative 260 meters per second, times cos of five degrees for the x-component of the plane with respect to the wind velocity. This works out to negative 225.203 meters per second. Then we do the same kind of work for the y-component, noticing that both of the blue and green vectors have y-components that are directed downwards. So they’re both negative, so put negative signs in front of each of those. And then these are both opposite components of their respective velocity triangles. So we're using the sine function to get it then. So we have negative 260 meters per second times sine of five degrees, minus 35 meters per second times sine of 15. Giving negative 31.719 meters per second. Then to find the resultant magnitude or the speed of this resultant, we take the square root of the sum of the squares of the components of this plane with respect to the ground velocity. So that’s the square root of negative 225.203 meters per second squared, plus negative 31.719 meters per second squared, giving 227 meters per second. And then we need to know what the direction is. So we take the inverse tangent of the y-component divided by the x-component. And that'll give us the angle that’s in here. Maybe I should write that in red, so this angle here. This is the angle of the plane with respect to the ground. It’s going to be opposite this y-component of the plane with respect to the ground velocity and adjacent to this x-component of the plane with respect to the ground velocity. So we take the inverse tangent of the y divided by the x-components and we get this angle. And we can ignore the negative signs, because we've already taken care of what the direction is by looking at this picture. We're going to label this as such and such number of degrees to the south of west, because we're measuring it to the south compared to west. So it’s the inverse tangent of 31.719 divided by 225.203 giving us 8.0 degrees. So the final answer for the velocity of the plane with respect to the ground is 227 meters per second, eight degrees south of west. And the part B, it says is this what we expect? Well, we know that the wind should deflect the plane further south. Because the wind is somewhat to the south and it’s also somewhat to the east. So we expect it to slow down a bit as well, and so sure enough, we see that the angle eight degrees is more than the angle we had before, five degrees. nd so sure enough, it has been deflected towards the south. And we can compare the magnitudes here; the 227 meters per second should be less than what it started with, which was 260. So that's good too. And so yes, our result is what we expect.