Question
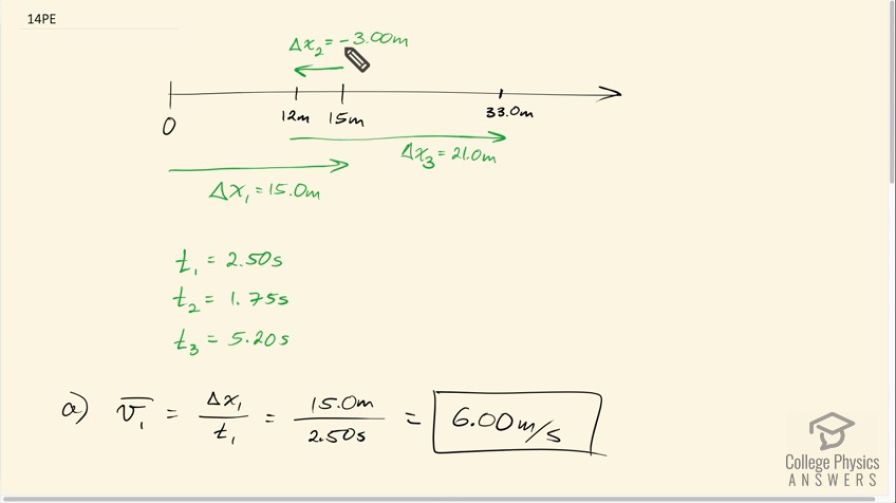
A football quarterback runs 15.0 m straight down the playing field in 2.50 s. He is then hit and pushed 3.00 m straight backward in 1.75 s. He breaks the tackle and runs straight forward another 21.0 m in 5.20 s. Calculate his average velocity (a) for each of the three intervals and (b) for the entire motion.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 2, Problem 14 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A football quarterback runs 15 meters downfield and then they are tackled taking them back 3 meters— that's what this negative sign indicates that the displacement during the second time period is to the left— but they break free of the tackle and then go forwards again 21 meters during this third time interval and so the question is what is their average velocity during each time interval, time 1, time 2 and time 3, and we are given the amounts of time for each of those time intervals. So what I have done here is I have written down all the things that we know and that's always a good way to start your question which is to write down the data that you are given. So the average velocity during the initial 15 meter run is that displacement divided by the time and I have subscripts 1 here to indicate we are taking values from the first time period. So that's positive 15 meters because the quarterback is running in the positive direction which we defined to the right divided by 2.50 seconds which is 6.00 meters per second and we can have three significant figures in that velocity since we have three significant figures in each of the displacement and the times. During the second time interval, the average velocity is Δx 2 divided by t 2 and during that time interval, the quarterback is being moved backwards and so there's a negative sign in front of this 3.00 meters and that lasts for 1.75 seconds this works out to negative 1.71 meters per second is their velocity. And then during the third time interval, the quarterback runs forwards so positive 21.0 meters in 5.20 seconds with an average velocity of 4.04 meters per second. Now part (b) asks what is the average overall velocity considering all three time periods and you must not take the average of these three numbers which might be surprising but these velocities persist for different periods of time and that's the reason you can't just take their average; this velocity persists for 2.50 seconds whereas this velocity goes on for 5.20 seconds. If you took a weighted average of these numbers weighted by the amount by which this time is a fraction of the total time then it would work out to the correct answer but you know, I think it's easier to explain how to find average velocity this way. So you find the total displacement and divide by the total time— that's the definition of average velocity— and so we have the displacement in the first time period is 15 meters plus the displacement in the second time period which is negative 3 meters and the displacement in the third time period is positive 21 meters so take that total and divide it by the total time and you get 3.49 meters per second— positive— is the average velocity overall.

