Question
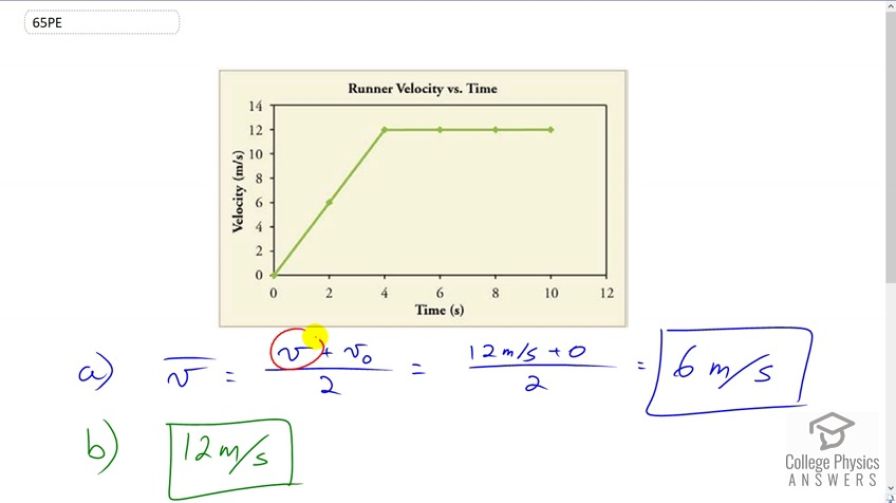
A graph of is shown for a world-class track sprinter in a 100-m race. (See Figure 2.79). (a) What is his average velocity for the first 4 s? (b) What is his instantaneous velocity at ? (c) What is his average acceleration between 0 and 4 s? (d) What is his time for the race?
Final Answer
a)
b)
c)
d)
Solution video
OpenStax College Physics for AP® Courses, Chapter 2, Problem 65 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. During the first four seconds of this race, the runner's average velocity is the final velocity plus the initial velocity divided by two. So final velocity we're speaking about here is the one that happens at four seconds and that is 12, which actually is the final velocity for the rest of the race too. In any case we have 12 plus zero the initial velocity, divided by two which makes six meters per second is the average velocity. Part B, asks us what his instantaneous velocity is at five seconds. So, we can take a tangent line at this particular point here but that tangent line would be just along here and it would be a horizontal line. We can see it with a -- actually, never mind about the tangent line, that will be for finding acceleration. No, no, no. What we have to do here is just read off the graph. Oh yeah. So at five seconds here, we just read what the y coordinate is, the y coordinate being the velocity and it is 12 meters per second. Then part C, what is the acceleration during the first four seconds. This is a slope question. What is the slope of the line here? We find it by calculating the rise over the run during the four seconds. The rise is the change of velocity going to the final velocity of 12, minus the initial velocity of zero. So here's the slope triangle. Then divide that by the time interval which is 4 seconds here. That gives us three meters per second squared acceleration. Part D is asking what is the time of the race. That is the easiest question because he starts at zero and he ends at 10 seconds. So, 10 seconds is the time of the race.