Question
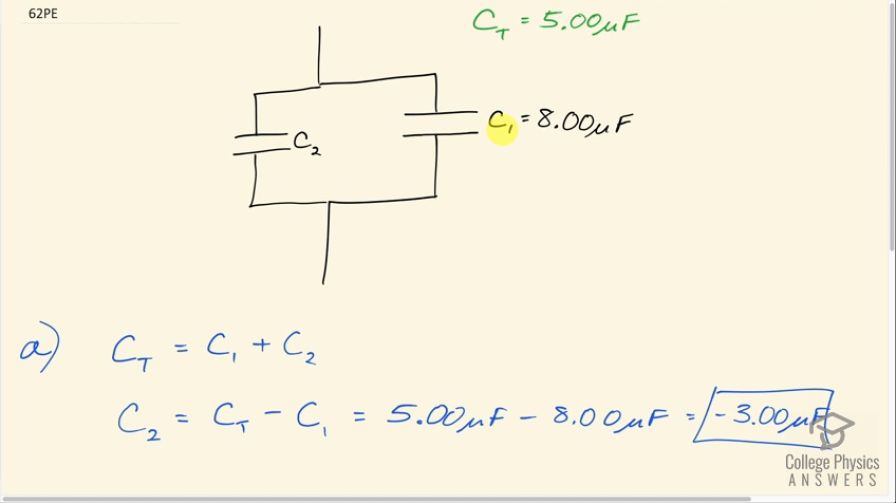
(a) An 8.00 μF8.00\textrm{ }\mu\textrm{F} capacitor is connected in parallel to another capacitor, producing a total capacitance of 5.00 μF5.00\textrm{ }\mu\textrm{F} . What is the capacitance of the second capacitor? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. −3.00 μF-3.00\textrm{ }\mu\textrm{F}
  2. A negative capacitance is not possible.
  3. When capacitors are connected in parallel, the total capacitance will always be greater than each single capacitance. 5.00 μF5.00\textrm{ }\mu\textrm{F} is too low for the total capacitance.

Solution video

OpenStax College Physics for AP® Courses, Chapter 19, Problem 62 (Problems & Exercises)

OpenStax College Physics, Chapter 19, Problem 62 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right
Video Transcript
This is College Physics Answers with Shaun Dychko. Two capacitors are connected in parallel and their total capacitance is 5.00 microfarads and capacitor, we'll call it C 1, is 8.00 microfarads and the question is, what is the other capacitor C 2? So the total capacitance because they are in parallel is the direct sum of each capacitance so C 1 plus C 2. So that means finding C 2 is found by subtracting C 1 from both sides and C 2 is the total then minus C 1. So that's 5.00 microfarads minus 8.00 microfarads which is a preposterous negative 3.00 microfarads. And the problem in this question then is that a negative capacitance is not possible so there's a problem with what we have been given here for our information. And when capacitors are connected in parallel, the total capacitance will always be greater than each single capacitance in the sum. And so 5.00 microfarads is too low for the total capacitance, it must be something more than 8.00.