Question
A system of three point charges has a 1.00 μC charge at the origin, a −2.00 μC charge at x=30 cm, and a 3.00 μC charge at x=70 cm. What happens to the total potential energy of this system if the −2.00 μC charge and the 3.00 μC charge trade places?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 19, Problem 12 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
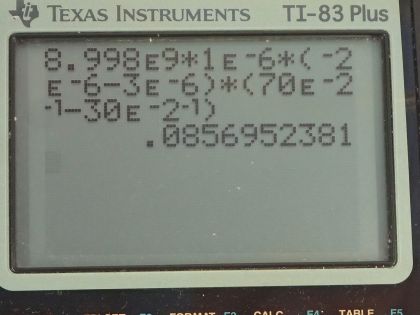
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have three point charges and this configuration of charge has a certain potential energy and the question is if we were to switch around charge two and charge three and position them this way, how would that change the potential energy of the configuration? So we'll figure out an expression for the potential energy of this original configuration and then make an expression for the switched configuration down here after switching q 2 and q 3 and then we'll subtract these two expressions and then calculate our answer. So when you are assembling a collection of charges, you imagine that the first one takes no work at all to put in place because there are no other charges in the universe we imagine and then we bring this second charge into its position and it will take some work to do that and the external work needed to move this charge from infinity where the potential energy is defined to be zero to this final position here... at constant speed by the way so this is the minimum amount of work possible to move from infinity to this position. This is going to be this PE 2—the potential energy of charge number two— and that will be its charge multiplied by the potential at this position due to this single charge q 1— q 3 is not part of the picture yet— and then after finding this potential energy of q 2 then with both these charges in place then we imagine bringing q 3 from infinity to this position here what will its potential energy be or in other words, what is the work done by an external force to move at a constant speed to this position? Now the potential energies are going to be negative because you know, the external work is going to be in the opposite direction to the displacement from infinity to this position Anyway... there's so many details I could get into but that might be a bit unnecessary. So to summarize, we begin with a charge here, we introduce q 2 and it will have a potential energy equal to its charge multiplied by the potential due to the single charge q 1 and then with these two charges in place then bring this q 3 into place and it will have a potential energy equal to q 3 times the potential of this position which we call v 3 and it will be a potential due to both these charges q 1 and q 2. Okay! So a potential energy of charge two when only charge one is present is q 2 times Coulomb's constant times q 1 over this distance x 2 and then the potential energy of charge three is gonna be q 3 times the potential at position three due to both charges one and two and so we have q 3 times kq 1 over x 3— this is the potential at position three due to charge one— plus kq 2 times x 3 minus x 2 and that's this distance here between charges three and two... this is x 3 minus x 2. Then we can factor out the Coulomb's constant from both terms and we have kq 3 times q 1 over x 3 plus q 2 over x 3 minus x 2. So the potential energy then in the original case is going to be the potential energy of bringing charge two into the picture when charge one is there already plus bringing charge three into the picture when charges one and two are already there and then we can factor out the k from all the terms here and multiply through by q 3 and then we have kq 1q 2 over x 2 plus q 1q 3 over x 3 plus q 2q 3 over x 3 minus x 2. There! Then we are going to switch charges two and three so now q 3 has moved to this position and it has a position x 3 prime to distinguish it from the x 3 before. So x 3 prime is 30 centimeters so this is the position of charge three after switching and that's 30 centimeters and then x 2 prime is now 70 centimeters and the potential energy in this new case after switching, which I am labeling with a prime, is going to be the same expression but now we have x 2 prime instead of x 2 and we have x 3 prime instead of x 3 and this is not just a 1-for-1 substitution these terms are also switched around because the distance here... we want the positive distance and so it is going to be x 2 prime minus x 3 prime in this denominator here. Okay! Now x 2 prime is what x 3 was before— x 2 prime is 70 centimeters and x 3 before was 70 centimeters— so let's replace x 2 prime with x 3 and x 3 prime is what x 2 was before so we are doing some replacements now. So x 2 prime is x 3 and we have x 3 here as well and x 3 prime is now x 2 so we have an x 2 here and an x 2 here. Then the change in potential energy, which is what the question is asking, is this potential energy prime after switching minus the potential energy originally and so we have kq 1q 2 over x 3 plus these two terms all of this is PE prime copied where I have multiplied through by Coulomb's constant and then subtract from that the potential energy expression before switching here that's copied here and I multiply through by Coulomb's constant as well and then getting rid of the brackets by distributing the negative into the terms there we have this line here and then we can factor out Coulomb's constant from every term we can factor out q 1q 2 from this term and this term so we have q 1q 2 times 1 over x 3 minus 1 over x 2 and then we can factor out q 1q 3 from this term and this term. So we have q 1q 3 times 1 over x 2 minus 1 over x 3 and then these two terms are equal with opposite signs and so they make zero. And we can make this a little bit more simpler still by multiplying this term by you know, the number 1 of course... you know, we can multiply anything we want by 1 and we are going to do it in a strategic way to make a bit more factoring... we are going to multiply by negative 1 twice so we are multiplying by negative 1 here and then we are multiplying in the bracket by a negative 1 which is to say that this q 1q 3 becomes minus and then these terms switch their signs and so we have 1 over x 3 minus 1 over x 2 and then a negative q 1q 3 and so q 1 by the way gets factored out completely from both terms and so we have kq 1 on the outside here and then we have q 2 positive and then a minus q 3 all multiplied by 1 over x 3 minus 1 over x 2 and then we can plug in numbers so we have Coulomb's constant times q 1, which is 1.00 microcoulomb times negative 2.00 microcoulombs minus 3.00 microcoulombs— that's q 2 minus q 3— times by 1 over 70 centimeters minus 1 over 30 centimeters and of course you know, I am speaking the prefixes that the question is giving us but I am writing the substitutions with their powers of 10 that the prefix means so 'micro-' means 10 to the minus 6 and 'centa-' means 10 to the minus 2 we end up with 8.6 times 10 to the minus 2 joules is the change in potential energy that's positive, which means that we have increased the potential energy with this new configuration.