Question
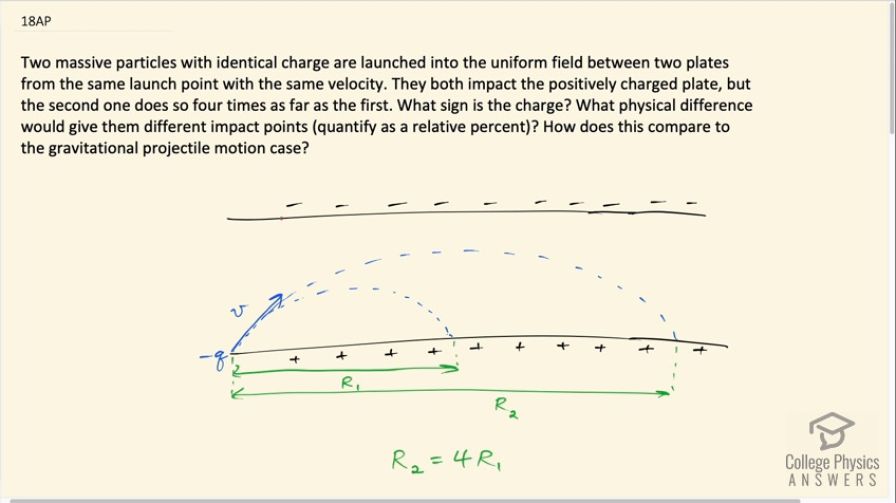
Two massive particles with identical charge are launched into the uniform field between two plates from the same launch point with the same velocity. They both impact the positively charged plate, but the second one does so four times as far as the first. What sign is the charge? What physical difference would give them different impact points (quantify as a relative percent)? How does this compare to the gravitational projectile motion case?
Final Answer
- The particle that travels further has 300% more mass than the particle that travels the shorter distance.
- With gravitational projectile motion, mass doesn't affect the range.
Solution video
OpenStax College Physics for AP® Courses, Chapter 19, Problem 18 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. Two particles that have the same charge are launched in this electric field here between two parallel plates so there's an electric field directed upwards here and since the particles have the same velocity that's to say that they have the same launch angle and the same speed but they go different distances and since their charge is the same and their velocity is the same, the only way to account for this difference in range is by a difference in mass of the particles. Now that might seem a little bit counter-intuitive because when you talk about range in terms of projectiles being influenced by gravity, it turns out that mass does not matter but in this question, we are going to ignore gravity and the force due to this electric field is going to be much more significant than gravity will and also if you try to solve this using gravity, you will end up not being able to get an answer so that's another reason why you have to ignore gravity. If you are like me, you are a little bit confused by this massive term here by saying they are massive particles that said to me, well, I should consider gravity and I actually solve this first of all using gravity in my free body diagram and then came to an impasse so anyway, we are not going to talk about gravity and it does, well, until the end, because it does ask us to compare to the projectile motion when you have gravity. Okay! So the range of the second particle is four times the range of the first particle— that's what we are told in this question here. Now the sign of the charge, it has to be well... since the charge impacts the positively charged plate, the sign of the charge has to be negative because if it was a positive charge then it would be repelled from the positive plate so we know the sign of the charge is negative. And now we are going to create an expression for the range and then it will be in terms of mass and then we'll see how the mass differs... we'll quantify the difference in mass as a relative percent. Okay! So the free body diagram, as I said, includes only the force due to the electric field, which is the charge multiplied by the electric field strength and here's Newton's second law, which says that the net force— of which there's only one— equals mass times acceleration and this is the vertical component of its acceleration... of course it's the entire acceleration because there's no horizontal acceleration at all. Okay! So we replace F e with qE and then solve for the vertical acceleration by dividing both sides by mass the vertical acceleration then is negative times the charge times the electric field strength divided by its mass. The particle's range will be the x-component of its initial velocity multiplied by time and we can say this because there's no horizontal acceleration so it's moving at constant speed horizontally speaking and then multiply it by time to get the range of course we don't know what the time is but we can figure it out in terms of things that we do know. So the vertical displacement which is zero because this projectile returns to the same vertical position as it started with so its vertical displacement is zero, it equals the initial y-component of its velocity multiplied by time plus one-half times its vertical acceleration times time squared— this is one of our kinematics formulas from chapter three or so— and well since this all equals zero, we can divide both sides by t and then afterwards subtract... (I guess I have done a couple of things at once here, let's do it in two steps) Well, let's write down that so v y plus one-half a yt equals 0— that's what happens when you divide both sides by t— and then we subtract v y from both sides and then multiply both sides by 2 over a y so you end up with this here— expression for time— negative 2v y over a y and a y is negative qE over m. Now if we are going to divide by this fraction, let's instead multiply it by its reciprocal in order to avoid the mess of having a fraction divided by a fraction. So we are multiplying by this flipped over so that's negative 2v y times m over negative qE and this works out to 2v ym over qE. So that's an expression for the amount of time that the projectile spends in the air and we substitute that in place of t in our range formula. So the range then is v x times 2v ym over qE and the range two is four times the range of particle one. So we have 2v xv y times m 2 over q E equals 4 times 2v xv ym 1 over qE the only difference between this here and the part in the brackets is the subscript on the m because the charge is the same for both particles, the electric field strength is the same and the initial velocities are the same the x-component and y-component of their velocities are the same so there's no need for subscripts one or two on any of those factors only on the mass and so everything cancels except for the masses and this number 4 so mass two is 4 times mass one. Now since the question is asking us for a relative percent, I am going to take that to mean percent difference and so we'll take m 2 minus m 1 over m 1 times 100 percent and that's 4m 1—is what m 2 is— and then minus m 1 is 3m 1 over m 1 is 3 times 100 percent that is 300 percent. So mass two of particle two is 300 percent more than particle one and then the other part of the question is compare to projectile motion with gravity. So with gravitational projectile motion, mass doesn't matter and you might recall that the range formula is initial speed squared times sin of 2 times the launch angle divided by acceleration due to gravity g and m does not appear anywhere there. We could have written this range formula to look a little bit more similar to this one by applying a trigonometric identity and we could have created expressions for these components and this is just for fun by the way— this is not necessary but v x would be v naught times cosine of the launch angle and then we have this factor 2 that's there and then times v naught times sin Θ—this is the y-component— and then we're multiplying all this by m and let's divide it by qE we could have written this as v naught squared because it's v naught times v naught here times sin of 2Θ and all this is times m divided by qE— this will be a range formula for a projectile that ignores gravity and is in the presence of an electric field and where I applied this trigonometric identity of sin 2Θ equaling 2 times cos Θ times sin Θ. Okay!