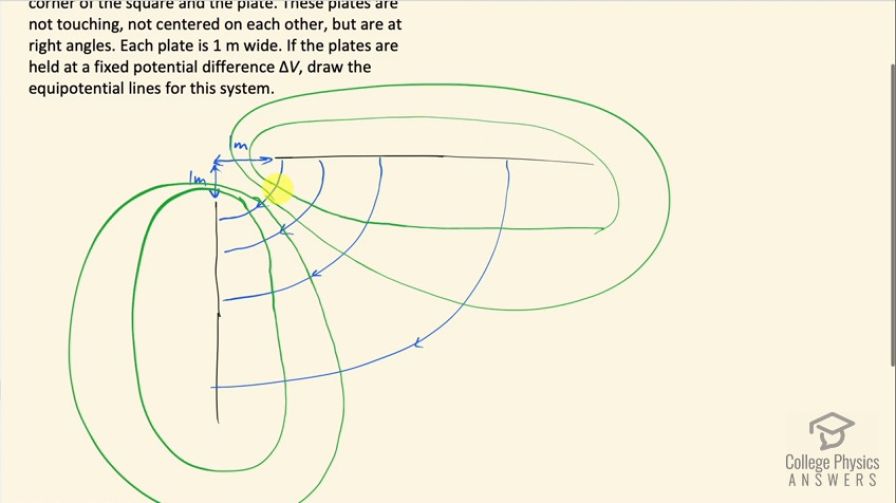
Question
Consider two conducting plates, placed on adjacent sides of a square, but with a 1-m space between the corner of the square and the plate. These plates are not touching, not centered on each other, but are at right angles. Each plate is 1 m wide. If the plates are held at a fixed potential difference , draw the equipotential lines for this system.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 19, Problem 26 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two plates that I have drawn black that are at right angles to each other and these blue lines represent the electric field between them this one is at a high potential and this one is at zero and so this is the positive plate I guess and this one's negative. Now these field lines go from the positive plate to the negative one and when the field line is close to their respective plates, the line is pretty much directly away from the plate so if you zoom in on just this little section here the field line is away from the plate because a positive test charge—if one was put here— would be pushed directly away strongly by this plate and this negatively charged plate far away from this point wouldn't matter and so the force would be directly away and likewise having a test charge here will be attracted directly towards this negatively charged plate and the positive plate being far away wouldn't matter and so the field line is directly towards the negative plate at this position. And then in between, it's some combination of the two so here would be a perfect diagonal because it will be equally repelled and attracted by these two different plates. So that explains this field line here and as you go further away, the field lines are going to be spaced further apart because each... the difference in electric field strength is the same between each of these lines and so in order for in order for that to work, these lines have to be spaced further and further apart since when you are really far away from both the plates, you are gonna get less of an electric field as this distance between the plates increases. So the difference between electric field lines is the same but the strength of the field changes and reduces as you go further towards these ends of these sides. Alright! The equipotential lines one way to think about how to draw them is that they must always be perpendicular to the electric field lines because the idea is that if you were to move a charge along an equipotential line, it would take no work to do that and this is the meaning of equipotential is that every position along this line is at the same potential, which means there is no work needed to move from one position to another along this line and so it has to be perpendicular to this electric field because if you went into any extent parallel to the electric field, you would have to do work against the field or with the field... one way or the other but you would have to do some work to move along the field line and so this is why equipotential lines are always at right angles to the field lines so as you are drawing these equipotential lines, you can think about that keeping it perpendicular as much as you can. So you know as you go further away from this corner, the equipotential lines are being spread apart just like the plates are and then when you have the plates close together, you have, you know, a high electric field and so there's going to be many densely packed isolines of potential here. There! That's good enough I think.