OpenStax College Physics for AP® Courses, Chapter 19, Problem 34 (Problems & Exercises)

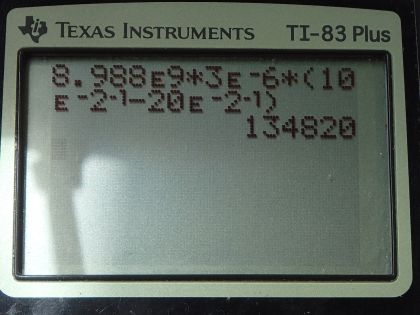
This is College Physics Answers with Shaun Dychko. We are interested in two points, A, and point, B, that are 10.0 centimeters and 20.0 centimeters respectively, away from this charge q of 3.00 microcoulombs. So the potential difference between point A and B is gonna be the potential at point A minus the potential at point B. So at point A, the potential is Coulomb's constant times the charge divided by the distance to A, which we will call r A, and then minus the potential at position B, which is kq over the distance to point B. We can factor out the kq and write it as multiplied by 1 over r A minus 1 over r B. And so this is Coulomb's constant times 3.00 microcoulombs (that should be a coulomb there) and then times 1 over 10 times 10 to the minus 2 meters minus 1 over 20 times 10 to the minus 2 meters and this works out to 135 kilovolts. Part (b) says suppose there is some potential which we'll call V AB prime, which is 2 times the V AB we found in part (a). So V AB prime is gonna be kq times 1 over r A minus 1 over r B prime so this is a new distance to point B. So this point B is being moved some distance away such that the potential difference between the new position B, B prime suppose, and A is twice the potential difference between point B and A. Now V AB prime divided by V AB is gonna be all of this which is V AB prime divided by V AB which is here. And V AB prime is 2 times V AB and so we make that substitution and so this left side works out to 2 because the V AB's cancel and then we multiply both sides by this denominator and then switch the sides around so we have this unknown r B prime on the left and we have 1 over r A minus 1 over r B prime equals 2 times this denominator that got multiplied by both sides 1 over r A minus 1 over r B. And then you could... (how do I explain this?) you could move this to the right hand side by adding it to both sides and then move this to the left hand side by subtracting it from both sides and then switch the sides around and you get 1 over r B prime equals 1 over r A minus 2 times 1 over r A minus 1 over r B. And then distribute this minus 2 factor into the brackets and you have 1 over r A minus 2 over r A plus 2 over r B and this will make minus 1 over r A which we put here so 2 over r B minus 1 over r A is 1 over r B prime. And then r B then is all of this to the power of negative 1 because that's how you flip a fraction is raise it to the exponent negative 1— take its reciprocal, in other words— and the right hand side we will also raise to the exponent negative 1. So we have 2 over 20 centimeters— r B being 20— minus 1 over r A, which is 10 centimeters to the negative 1 but this 2 over 20 is 1 over 10 so this is 1 over 10 minus 1 over 10 which is 0 to the negative 1 and you can't raise zero to the exponent negative 1— it's undefined— or the physical interpretation is that this is infinity. So r B prime is some distance as far away as possible... that's where you will get a potential difference between r B prime and A equal to twice the potential difference between B and A.