Question
A system of three point charges has a 1.00 μC charge at the origin, a −2.00 μC charge at x=30 cm, and a 3.00 μC charge at x=70 cm. What is the total stored potential energy of this configuration?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 19, Problem 10 (Test Prep for AP® Courses)
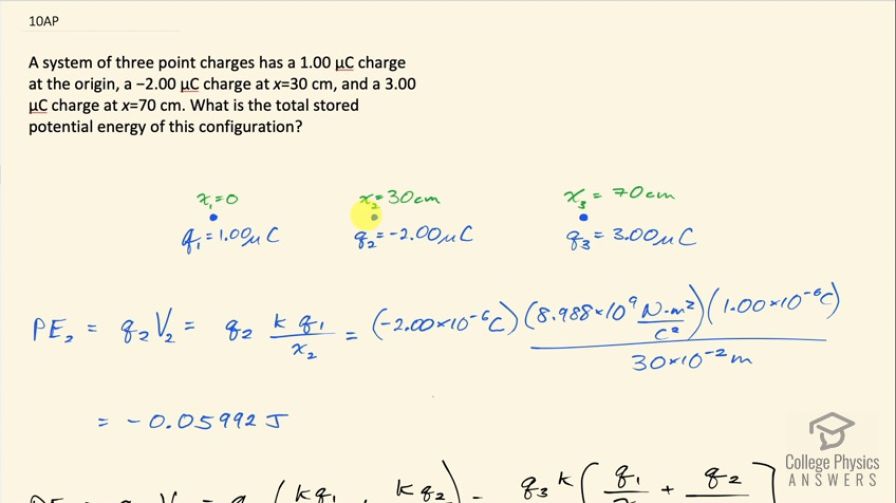
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are given three point charges this one at the origin has a charge of 1.00 microcoulomb, there's a charge two here at 30 centimeters away with a charge of negative 2.00 microcoulombs and a third charge 70 centimeters away from the origin with a charge of 3.00 microcoulombs and we are asked what is the total potential energy stored in this configuration of charges? So another way of asking that is how much work would an external force need to do to assemble these three charges in this configuration. So we can imagine that we start with this charge here to begin with and then it takes no work to put charge one here since we imagine that there's no other charges in the picture yet and then we introduce charge two starting from infinity and then some external force does some work to bring that charge to here but since the charge is negative, the electrostatic force of course is attractive so the external force would apply a force directed towards infinity so this would be some external force. I am getting a little bit theoretical here but maybe that will help help you understand what the algebra that's coming up here... well... I shouldn't say algebra but more just the calculations coming up there's no real algebra. So we imagine that this charge two— and then charge three is not part of our picture yet by the way— so we have this charge two at infinity and it's gonna come towards charge one and this force external is going to apply a force away from charge one in order for this to be at constant speed because when we are talking about potential energy, we are talking about this external force operating such that the movement happens at constant speed and what I haven't drawn though is this electrostatic force of attraction here— that's the electrostatic force— and so the external force would be equal to the electrostatic force. So we are building this charge configuration how much work does this external force need to do to create this configuration of charge that we want? So we need to know what is the potential of our destination position and that's what this formula here is all about this formula tells us what is the potential due to this point charge at this position x 2. Okay... let's get this back into position here so we have got this charge number two at its final position of x 2, this external force did some negative work and so that's part of my point here too is that I am trying to explain why this is a negative amount of potential energy because this external force has done a negative amount of work since the displacement has been towards charge one and yet the force has been away from charge one in order to balance the attractive electrostatic force in order to maintain a constant speed. Okay! So... when we are finding the amount of potential energy needed to do this, we are only thinking about the potential due to charge one, charge three is not yet part of our picture and so we have charge two multiplied by the potential at this position two and that potential is due to charge one so that's kq 1 over the distance, which is x 2 here and all that gets multiplied by q 2 to turn it into an energy in joules, so it's not a voltage... this fraction here is the voltage and then multiplying it by this charge gives the amount of energy then to bring this charge here from infinity. Okay! So we have negative two times 10 to the minus 6 coulombs times the Coulomb's constant times 1.00 times 10 to the minus 6 coulombs—charge one— divided by 30 centimeters, which is 30 times 10 to the minus 2 meters and that is negative 0.05992 joules. Then we want to bring charge three into the picture so it starts way off at infinity and then it's brought closer and closer and there's a negative amount of work being done in this case too since this charge c is a net negative charge among these two since this is negative 2.00 and this is positive 1.00 so that makes a net charge of negative 1.00 here so there's a negative amount of work done in this case too and the amount of work will be this charge q 3 multiplied by the potential of this position. Now the potential of this position is now due to two charges: there is q 1 creating a potential at this position and also charge two creating a potential at this position. So when we find the potential energy to bring charge three into the picture, we have to multiply q 3 by the potential due to both of the charges that are there already— q 1 and q 2. So we have q 3 times k times q 1 over q 3 or x 3 I should say plus q 2 over the distance between charge three and two, which is x 3 minus x 2. And so that's 3.00 times 10 to the minus 6 coulombs times Coulomb's constant times 1.00 times 10 to the minus 6 coulombs divided by 70 centimeters plus negative 2.00 times 10 to the minus 6 coulombs divided by 40 centimeters, which is 70 minus 30 centimeters written as meters of course and this is negative 0.0963 joules. So the total potential energy will be the sum of these two potential energies and that is negative 0.156 joules.

