Question
An advertisement claims that an 800-kg car is aided by its 20.0-kg flywheel, which can accelerate the car from rest to a speed of 30.0 m/s. The flywheel is a disk with a 0.150-m radius. (a) Calculate the angular velocity the flywheel must have if 95.0% of its rotational energy is used to get the car up to speed. (b) What is unreasonable about the result? (c) Which premise is unreasonable or which premises are inconsistent?
Final Answer
- The centripetal acceleration of a point on the edge of the disk is . The material of the disk will not be able to provide the force needed to sustain this centripetal acceleration. The spinning disk would break into pieces spinning at this speed.
- The flywheel needs to have a much greater mass and radius.
Solution video
OpenStax College Physics for AP® Courses, Chapter 10, Problem 20 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
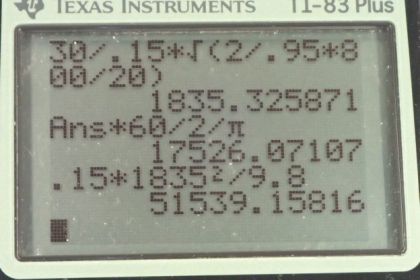
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An 800 kilogram car can supposedly be accelerated from 0 meters per second up to 30 meters per second by a flywheel that has a radius of 15 centimeters which is 0.150 meters and a mass of 20 kilograms. So this radius is really small— it's half the length of this school ruler— so we should be skeptical that this is gonna work especially since parts (b) and (c) of this question say what's unreasonable about the result and so on? Okay! So the idea is that the kinetic energy... the rotational kinetic energy of the flywheel is going to get turned into translational kinetic energy of the car. So here's its translational kinetic energy: one-half mv squared— this is mass of the car and its final speed squared— and over here, we have 95 percent of the rotational kinetic energy is gonna get translated into this translational kinetic energy. Okay! So the rotational kinetic energy is one-half times moment of inertia times the angular speed squared. Now for the moment of inertia, we need to consult our list of formulas and this flywheel is a disc that is solid and so its formula is going to be mass times its radius squared over 2 so we make that substitution here so we have mass of the wheel times its radius squared divided by 2. And we are solving for ω here— we want to know what the angular speed is— so we are going to multiply the 2 together that makes 4 and then multiply both sides by 4 which cancels with this 2 down here to make 2 in the numerator 4 divided by 2 is 2 and then we are also dividing both sides by 0.95 which just gets copied here and we are dividing by mass of the wheel both sides and dividing by r squared on both sides and times by 1 over mass wheel r squared and then we have this line here then we take the square root of both sides to solve for the angular speed. So square rooting these two factors and then bringing them out of the square root sign, we have this line here which says that the angular speed that the wheel had initially is the final translational speed of the car divided by the radius of the flywheel times the square root of 2 over 0.95 times mass of the car divided by mass of the wheel. So that's 30 meters per second divided by 0.150 meters—radius— times square root of 2 over 0.95 times 800 kilograms—mass of the car— divided by 20.0 kilograms— mass of the flywheel— and that's 1835 radians per second has to be the spin speed of the wheel. We'll turn that into rpm to have a better sense of what that number means so we multiply by 60 seconds per minute and then by 1 revolution for every 2π radians and we have 17500 rpm. Now that's really fast and we can get a sense of how fast that is by thinking about what the centripetal acceleration of a point on the edge of the flywheel would be. So centripetal acceleration is the tangental velocity squared over r and then we can substitute r times angular velocity in place of v and then square that and divide by r and we have r to the power of 1 times ω squared. So that's 0.150 meters times this radians per second we got up there, square that, turn it into g's— 1 g for every 9.8 meters per second squared— this is 51500 g's. That's incredibly large so this disk is spinning so fast that it would break apart into pieces. There's no way that the bonding force between the material itself of the flywheel would sustain this type of acceleration for the bits that are on the edge of the flywheel. So in order for this advertisement to be true to have 95 percent of the flywheel's rotational kinetic energy accelerate the car from 0 to 30, the flywheel needs to have a much greater mass and radius and you can see that from here. So this angular speed gets reduced when you increase this denominator— this is the radius of the flywheel— and it also gets reduced when you increase the mass of the flywheel. Now since the mass of the flywheel is under the square root sign, increasing the radius will have a greater effect but both will, nevertheless, reduce ω.