Question
A ball with an initial velocity of 8.00 m/s rolls up a hill without slipping. Treating the ball as a spherical shell, calculate the vertical height it reaches. (b) Repeat the calculation for the same ball if it slides up the hill without rolling.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 10, Problem 28 (Problems & Exercises)
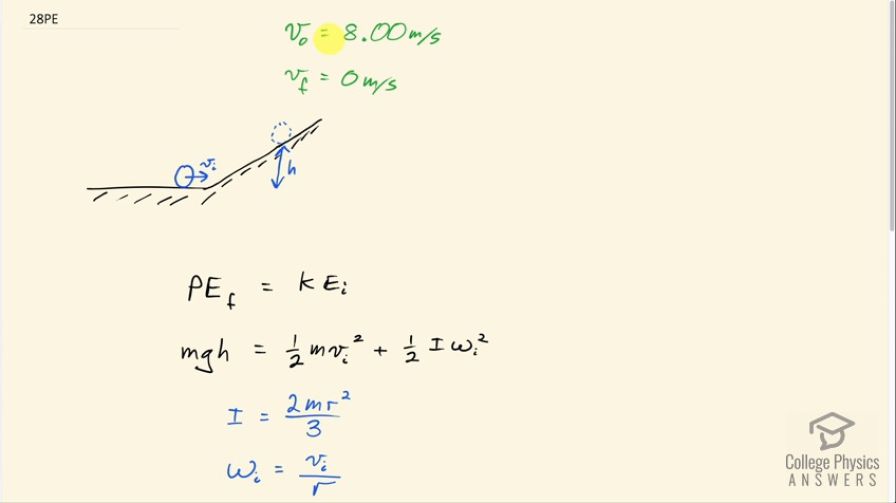
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This ball is going to roll without slipping up this hill and it has an initial velocity of 8.00 meters per second and the question is what height will it reach at which point its final velocity will be zero? Now we know that the final potential energy that it will have here is going to equal the initial kinetic energy that it has here. Now there's no kinetic energy here at this point because it's not moving and at this point, there's no potential energy because we'll take this to be our reference level; we'll say that our height equals zero at this point so that's why there's no potential energy term here because it's just zero and likewise, there's no kinetic energy term here because it's zero as well. Okay! So we have the potential energy at the final time is mgh and initially, there are two types of kinetic energies: there's translational kinetic energy, one-half mass times velocity initial squared; and there's also rotational kinetic energy, one-half times moment of inertia times angular velocity squared. Now because the ball is not slipping that means we can say that the angular velocity is the translational velocity divided by its radius and the question tells us to treat this ball as a thin spherical shell and so we have to consult our formulas to find out what the moment of inertia formula is and it's 2 times mass times radius squared divided by 3. So we plug in both of these things here. So we have mgh equals one-half mv i squared plus one-half times 2mr squared over 3 times—the angular velocity— v i over r squared. m is a common factor that cancels everywhere when you multiply both sides by 1 over m. This radius in the denominator is squared and so it cancels with this radius squared in the numerator— this 2 cancels with this 2— and we are left with v initial squared over 3 from that term and we are left with v initial squared over 2 here. And multiply this by 3 over 3 and this one by 2 over 2 and we end up with 5v i squared over 6 equals gh. So then divide both sides by g and we have the height then is 5 times v initial squared over 6 times g. So that's 5 times 8.00 meters per second squared divided by 6 times 9.80 meters per second squared and that is a height of 5.44 meters.

