Question
This problem considers additional aspects of example 10.7, Calculating the Effect of Mass Distribution on a Merry- Go-Round. (a) How long does it take the father to give the merry-go-round an angular velocity of 1.50 rad/s? (b) How many revolutions must he go through to generate this velocity? (c) If he exerts a slowing force of 300 N at a radius of 1.35 m, how long would it take him to stop them?
Final Answer
Solution video
OpenStax College Physics, Chapter 10, Problem 10 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
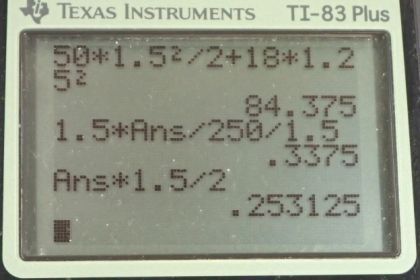
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In example 10.7, we had a problem where a father was pushing this merry-go-round around and his child is sitting a distance 1.25 meters from the center; the child has a mass of 18.0 kilograms and I have the variables related to the child with the subscript c for child and then the merry-go-round itself is 50.0 kilograms in mass and it has a radius of 1.50 meters. The father pushes with a force of 250 newtons and does so in a direction that's perpendicular to the radius. So this merry-go-round is starting from rest and has a final angular velocity of 1.50 radians per second and part (a) asks us how long will it take to reach that final angular velocity? So we have final angular velocity is initial angular velocity plus angular acceleration multiplied by time and we can solve for t by subtracting ω naught from both sides and then dividing both sides by α and then switching the sides around. So we have t is ω f minus ω naught divided by α. Now it's gonna take some work to figure out what this α is. We have this Newton's second law analog for rotational systems is that the net torque is the moment of inertia multiplied by angular acceleration and we can solve for α by dividing both sides by I. We can find the torque because that's this force that the father applies multiplied by the distance to the center and we can also find the moment of inertia. So we have that the torque is, you know, the force times the radius and the moment of inertia is going to be— after we consult with our formulae, we have to figure out which of these formulas apply to this situation; what we have is a solid cylinder, it's a very thin cylinder a disc, in other words, and it's gonna have this formula: mass times its radius squared divided by 2... that's its moment of inertia. So this accounts for the merry-go-round and then we have the moment of inertia of the child which we'll consider a point mass which has formula mr squared. So that's mass of the child times distance between the center and the child squared. I could plug this formula in for I here but then thing's gonna get really messy and have a lot of writing so let's just plug in numbers and figure out what this I is in a number form. So we have 50.0 kilograms times 1.50 meters squared divided by 2 plus 18.0 kilograms of the child times 1.25 meters squared gives 84.375 kilogram meters squared is the moment of inertia of this whole system— merry-go-round and child together. So the angular acceleration then is this torque— force times distance or lever arm— divided by this moment of inertia and then that's what we plug in for α in this formula for t. Now we are dividing by α and I don't like dividing fractions by fractions because I find that confusing so instead we are going to multiply by the reciprocal of this denominator so I am gonna multiply it by this α flipped over. So multiplying by 84.375 kilogram meter squared divided by force times lever arm. So this is 1.50 radians per second— final angular velocity—minus 0 times this moment of inertia divided by 250 newtons—the force applied by the father— times 1.50 meters— the distance from the center to where the force is applied— these are perpendicular and we get 0.338 seconds. Part (b) is asking us how many times how many revolutions will it make, how many times will it go around? So that's gonna be the average angular velocity multiplied by time so that's the initial plus final angular velocities divided by 2 multiplied by time. That's 0 plus 1.5 radians per second over 2 times 0.3375 seconds and that is 0.25313 radians which we convert into revolutions by multiplying by 1 revolution for every 2π radians so that's 0.0403 revolutions. Part (c) asks if he exerts a new force that's 300 newtons at a distance 1.35 meters from the center and where you presume that this force is perpendicular to the radius, how long will it take him to stop the merry-go-round? So we are borrowing this formula for time from up here and time then is final angular velocity minus initial divided by α— α is the torque divided by moment of inertia— and so then we are multiplying by the reciprocal of this angular acceleration and so we're multiplying by I over < i>F r. So that's 0—final angular velocity because it's coming to a stop— minus the 1.50 radians per second— initial angular velocity here— times the moment of inertia divided by this negative torque and we'll call it negative because it's in a direction opposite to our initially positive angular velocity. So it's negative 300 newtons times 1.35 meters which is 0.313 seconds to bring the merry-go-round to a stop.