Question
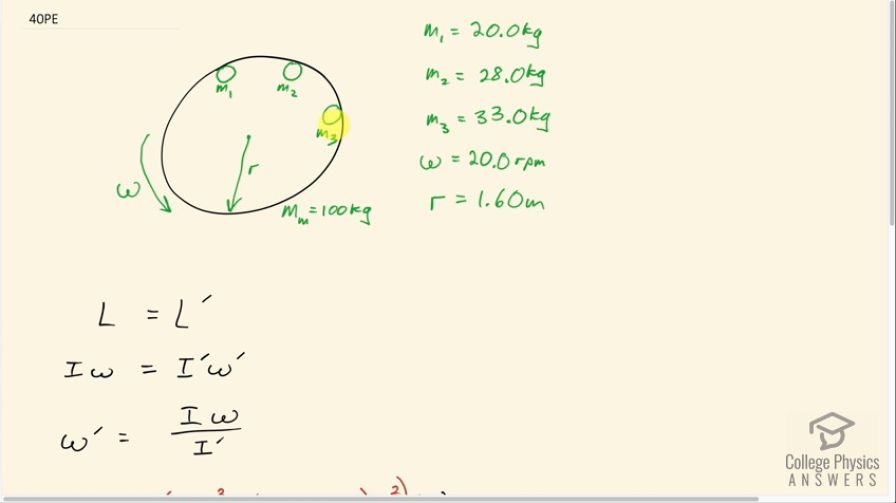
Three children are riding on the edge of a merry-go-round that is 100 kg, has a 1.60-m radius, and is spinning at 20.0 rpm. The children have masses of 22.0, 28.0, and 33.0 kg. If the child who has a mass of 28.0 kg moves to the center of the merry-go-round, what is the new angular velocity in rpm?
Final Answer
Solution video
OpenStax College Physics, Chapter 10, Problem 40 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a merry-go-round that's spinning with a speed of 20 rpm and there are three children on the outer edge with masses 20.0 kilograms, 28.0 kilograms and 33.0 kilograms and the merry-go-round itself has a mass of 100 kilograms and it has a radius of 1.60 meters. So we have written down all the things that we know; we are not gonna bother converting this unit into radians per second because the question asks us for the answer in rpm and it's okay to work with rpm instead of radians per second here and I'll show why in a second. So we know that angular momentum has to be conserved when this mass 2— 28.0 kilogram child— moves to the center the system will still have the same total angular momentum and when this child moves to the center that's going to reduce the moment of inertia of the system because each of these children— each has a moment of inertia— we'll treat them as point masses of m 1r squared and m 2r squared and m 3r squared and then this when it goes to the center will have a radius of zero or a distance of zero from the axis of rotation and so its moment of inertia will be zero. So that's going to cause a compensating increase in angular velocity in order to maintain the same angular momentum so let's calculate what that new angular velocity will be. So the initial angular momentum equals the final angular momentum prime indicating after some event here— in this case, m 2 moving to the center— and the initial moment of inertia times angular velocity equals the final moment of inertia times angular velocity and we can solve for ω prime by dividing both sides by I prime and then we have to make substitution's for the moment of inertia in each case. So we have the merry-go-round in each case is like a disc and it has a formula mr squared over 2 because it's like a solid cylinder rotating about the central axis. And so mass of the merry-go-round times its radius squared over 2 is its moment of inertia and then add to that the moment of inertia of each of the three children. The r squared is a common factor that can be factored out so I write m 1 plus m 2 plus m 3 times r squared and all that gets multiplied by the initial angular velocity. And then we divide that by the final moment of inertia which is the same except this is lacking m 2 because that child moved to the center in which case their distance from the axis of rotation is zero making a moment of inertia of zero for that child. So we have a 100 kilograms— mass of the merry-go-round— times 1.60 meters—radius—squared over 2 plus 22.0 kilograms plus 28.0 plus 33.0 all times 1.60 meters squared times 20.0 rpm and yeah, we can leave this as rpm because what we have here is a bracket here with the same units as this factor below and the units in this bracket and this bracket are going to cancel because they are the same and they are being divided. The units are kilogram meters squared and so we'll end up multiplying this by a dimensionless factor and so that's not going to change the units; we can leave the units as rpm and we'll end up with rpm. Okay! So then we divide by the new moment of inertia after the child, m 2, goes to the center and we have 25.3 rpm will be the final angular velocity. And we expected this number to be larger than the initial and it is and so that's, you know, a sort of a reality check that you should do on your answers to make sure you have a sense as to whether it should be correct or not; if this number had been less than 20, we know that we would have made a mistake somewhere.
