Question
This problem considers energy and work aspects of Example 10.7—use data from that example as needed. (a) Calculate the rotational kinetic energy in the merry-go-round plus child when they have an angular velocity of 20.0 rpm. (b) Using energy considerations, find the number of revolutions the father will have to push to achieve this angular velocity starting from rest. (c) Again, using energy considerations, calculate the force the father must exert to stop the merry-go- round in two revolutions
Exerpt from Example 10.7
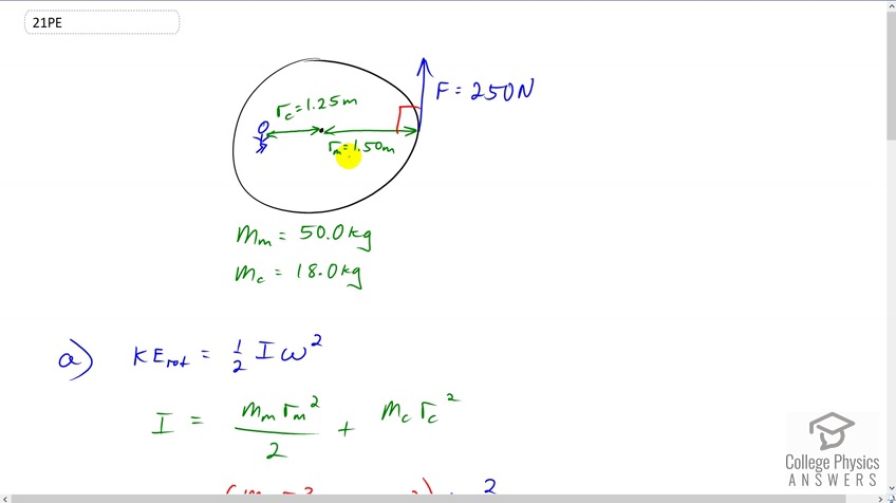
Consider the father pushing a playground merry-go-round in Figure 10.13. He exerts a force of 250 N at the edge of the 50.0-kg merry-go-round, which has a 1.50 m radius.Final Answer
a)
b)
c)
Solution video
OpenStax College Physics, Chapter 10, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A father is pushing the edge of a merry-go-round with a force of 250 newtons directed perpendicular to the radius, and the radius of the merry-go-round is one and a half meters. There is a child with mass 18 kilograms sitting one and a quarter meters from the center, and the merry-go-round mass itself is 50 kilograms. So our first question is to figure out what is the rotational kinetic energy of this system assuming that it has a angular velocity of 20 revolutions per minute. Rotational kinetic energy is one half times moment of inertia multiplied by angular velocity squared, and the moment of inertia of the system will be that of the merry-go-round which we modeled as a disc, plus the moment of inertia of the child which we modeled as a point mass. So we have substitution of both things in place of I, so we have merry-go-round mass times radius of merry-go-round squared over two plus the child mass times the child’s distance from the center squared and we multiplied that by angular velocity squared. So it’s one half times 50 kilograms times one and a half meters squared over two, plus 18 kilograms times one and a quarter meters squared, all times 20 rpm which is revolutions per minute and we have to convert that into radians per second by multiplying by 2 pi radians per revolution and then by one minute for every 60 seconds, and then we square that result, and we get 185 Joules as the rotational kinetic energy. Now in part b, we’re asked to figure out over how many rotations will the father have to push in order to achieve this final velocity of 20 rpm. So the net work done is the change in rotational kinetic energy and since it starts at rest, that term is zero, we just have one half I omega squared. And the net work done also can be thought of as the net torque multiplied by the angular displacement, and the torque is the force that the father applies times the radius of merry- go-round times theta. And so we can equate this and this since they both are equal to work net, and that’s what we do in this line, and then we solve for theta by dividing both sides by F rm. And so the angular displacement is I omega squared over two F rm, and then I substituted for moment of inertia just as we had before, there’s the disc of the merry-go-round plus the child’s moment of inertia. Then we plug in numbers, so that’s 50 kilograms times one and a half squared over two, plus 18 times 1.25 squared and then times by this angular velocity squared, divided by two times 250 newtons force applied, multiplied by one and a half meters, and we get this number of radians which we then have to convert into revolutions by multiplying by one revolution for every 2 pi radians. Then we end up with 0.0785 revolutions. And in part c, we’re asked if there were meant to be two full revolutions, or during which the father is stopping the merry-go-round given that it has an initial velocity of 20 rpm, what force would he have to apply. So I’ve taken this formula which we figured out using energy considerations already over here, and rearranged it to solve for F instead of theta. So F is going to be I omega squared over two radius of the merry-go-round times theta. And then plugging in all these numbers from moment of inertia as we have before and the angular velocity and divided by two times one and a half meters times two revolutions converted into radians by multiplying by 2 pi radians per revolution, then we end up with 9.82 newtons.


