Question
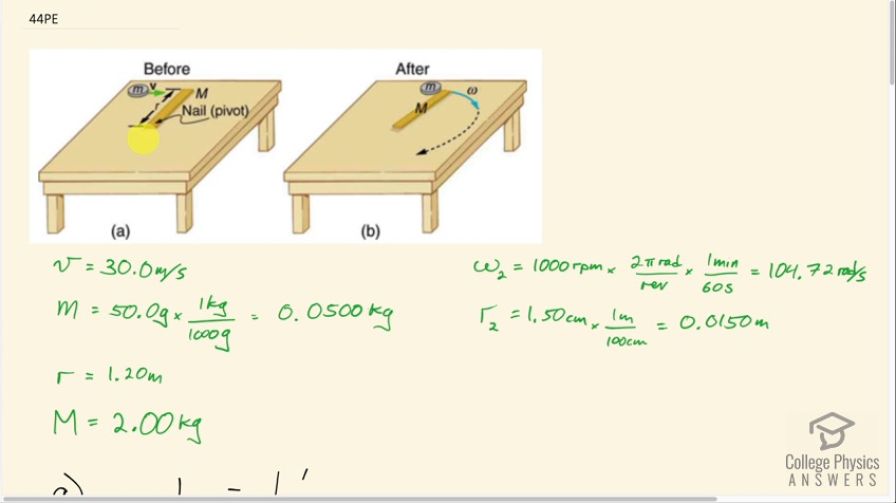
Repeat Example 10.15 in which the disk originally spins clockwise at 1000 rpm and has a radius of 1.50 cm.
Example 10.15
Suppose the disk in Figure 10.26 has a mass of 50.0 g and an initial velocity of 30.0 m/s when it strikes the stick that is 1.20 m long and 2.00 kg.
(a) What is the angular velocity of the two after the collision?
(b) What is the kinetic energy before and after the collision?
(c) What is the total linear momentum before and after the collision?
Final Answer
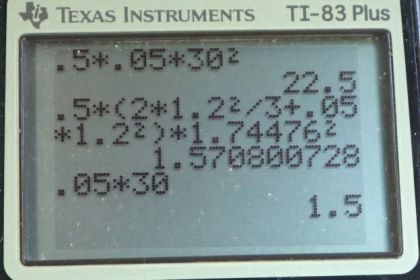
- , \textrm{KE}^ = 1.57\textrm{ J}`
- , = 2.20 \textrm{ kg}\cdot\textrm{m/s}` > p` since the nail exerts a torque during the collision.
Solution video
OpenStax College Physics, Chapter 10, Problem 44 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A disc with mass, m, which is 50.0 grams is approaching a stick that's initially at rest and it has a mass, M, which is 2.00 kilograms and the stick's length is 1.20 meters. This disc is gonna hit the stick and then stick to the stick and then it will go off together in this rotation because there's a nail here acting as a pivot. Now the disc is also spinning before it hits the stick and it's spinning at 1,000 rpm which we convert into radians per second by multiplying by 2π radians per revolution and then 1 minute for every 60 seconds and the disc we are told has a radius 1.50 centimeters which we will convert into meters and these have a subscript 2 so this is the angular velocity 2 of the disc initially and this is the radius of the disc, r 2. Okay! So our first job is to figure out what is going to be the angular velocity of this system after the disc is attached to the stick? So... we know that the angular momentum of the system before collision equals the angular momentum of the system after collision and before the collision, we have two angular momenta to consider: one is the movement of the disc which is a bit strange to think of it as an angular momentum because it's a linear momentum but at the very instant where the disc is just here before it's attached to the nail, we can imagine that it's going in this circle. You know, when it is moving in the circle, it has a tangental velocity and likewise when it's here just before attaching to the stick, it likewise has a tangental velocity just the same and so we can interpret that as an angular velocity as well. Okay! So that's L 1 and it's a point mass so its moment of inertia is mr squared and we multiply by its angular velocity which will be its approaching linear velocity divided by its distance from the pivot and then I substitute v over r in place of ω here and then I add to that the angular momentum of the disc spinning and the reason we can add these as scalars is because these vectors... these angular momentum vectors are both pointing in the same direction. If you were to grab this with your right hand, the disc... we are gonna assume that they are in the same direction so we'll assume that the disc is spinning this way and if you grab it with your right hand, your thumb is pointing down so the vector of the angular momentum is downwards. And then just before it hits the stick, we can imagine it rotating this way and then that angular momentum also is downwards. Okay so we can add those two together. So this is the moment of inertia of a disc which we get from here, mr squared over 2, and then we multiply that by ω 2, which is given to us, 1000 rpm. Okay so rewriting it with the substitution for the angular velocity of its movement around or its orbit around the nail and then these r's cancel— at least one of them anyhow—so we have mr times v plus mr 2 squared over 2 times ω 2. Okay! So that's the initial total angular momentum of the system. Then after the disc is attached to the stick, there's going to be a moment of inertia multiplied by this new angular velocity that we want to find, ω prime. The moment of inertia is going to be the moment of inertia of a stick rotating about an axis at the end and so that's going to be mass times its length squared over 3. So that's Mr squared over 3 plus this point mass of the disc at the end of it, mr squared, and so now we equate these two. So we have L prime which is all this equals the initial angular momentum which is L here and so we'll divide both sides by this bracket. And so we get the angular velocity, after collision, is mrv plus mr 2 squared over 2 times ω 2 all divided by this stuff here. Okay! So that's 0.0500 kilograms— mass of the disc— times 1.20 meters—disc's distance from the center or the nail— times 30.0 meters per second— initial velocity— plus the disc mass times the disc radius— 0.0150 meters—squared divided by 2 times the 1000 rpm converted into radians per second which is 104.72 radians per second. All that gets divided by the mass of the stick times the stick length squared over 3 plus mass of the disc times its distance from the nail—1.20 meters—squared. This gives 1.74 radians per second will be the angular velocity after the disc is attached to the stick. Okay! The kinetic energy of the system, before collision, is one-half mass times linear velocity squared so it's one-half times 0.0500 kilograms times 30.0 meters per second squared which is 22.5 joules. After collision, the kinetic energy is entirely rotational and so it's one-half times its moment of inertia times the angular velocity squared. So it's one-half times the moment of inertia of the stick plus the moment of inertia of the point mass disc times its angular velocity that we found in part (a) squared. So it's one-half times 2.00 kilograms times 1.20 meters squared over 3 times 0.0500 kilograms times 1.20 meters squared times this angular velocity with lots of decimal places because we don't want to have intermediate rounding error and you square that and you get 1.57 joules is the kinetic energy after collision. Part (c) asks us to compare the total linear momentum before and after collision. So before collision, it's straightforward: it's the mass of the disc times its velocity so that's 1.50 kilogram meters per second; after collision, we have the disc moving with a new tangental velocity v prime— that we'll have to figure out— and then we also have the stick moving and we are gonna consider it to be a point mass located at the center of mass of the stick and so its linear momentum will be its mass times the velocity of the center of mass after collision. So the velocity of the disc is going to be the radius— the distance from the nail to the disc— times its angular velocity that we found in part (a) and the velocity of the center of mass will be its distance from the nail which is the stick length divided by 2 because we assume the stick has uniform mass distribution, in which case, its center of mass is in its geometric center... we multiply it by its angular velocity after collision. So we make substitutions here for v prime and v CM prime then factor out ω prime r common factors here so we have ω prime r times mass of the disc plus mass of the stick over 2. So that's 1.74476 radians per second times 1.20 meters times 0.0500 kilograms plus 2.00 kilograms over 2 so that's 2.20 kilogram meters per second. Now it might be a bit of a surprise to see this being different from the initial linear momentum and the reason for that is that this stick is not isolated... the system is not isolated. The stick is attached to a nail and that nail is going to exert a torque during the collision which will speed up the rotation more than it would otherwise been had the nail not been there. There we go!