Solution video
OpenStax College Physics, Chapter 10, Problem 2 (Problems & Exercises)

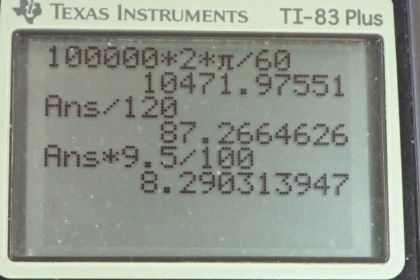
Calculator Screenshots
Comments
Can you help me? I am following the exact same steps of the video but on the HW page it still keeps telling me I'm wrong. The problem is set up the same, except my numbers are different. In my problem the ultracentrifuge accelerates from rest to 9.97x10^5 in 1.75 min (105s) and the point of axis of rotation is 8.50cm (0.850m). These are the answers I am getting for each part: a)99.4 b)8.45 c)9.27x10^6 d).9.46x10^5. All these answers when entered in the hw are wrong..
Hi aeresay, thank you for the question. Without getting too specific to your particular homework problem, consider working through the problem here, with the values in the question here, and see if you can arrive at the same answers as in the video. Working through it like that might reveal any errors.
All the best,
Shaun