Question
Prove that for any relative velocity between two observers, a beam of light sent from one to the other will approach at speed (provided that is less than , of course).
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 28, Problem 32 (Problems & Exercises)
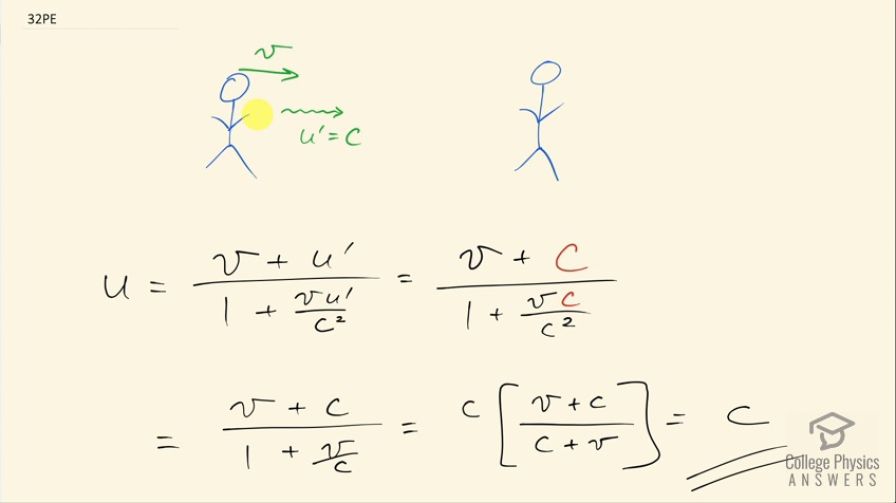
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to show that when two observers are approaching each other with a relative velocity of v that when light is emitted from one observer with a speed of c of course, we are going to show using this formula that the other observer will also report a velocity for this light as c. So suppose this first observer is labeled with the velocity v that means the velocity for the light that they report is labeled u prime and we are told u prime is c so the question is what velocity does the second observer report for this light? So the velocity that the second observer reports is going to be v plus u prime over 1 plus v times u prime over c squared. So u prime is c so we plug in c, wherever we see u prime here and this vc over c squared becomes just v over c and then we can multiply top and bottom by c and on the top, let's just leave it outside of some brackets and on the bottom, the c gets distributed into this binomial and so we have c plus c times v over c, which is just v and this numerator and denominator are the same so this fraction is 1 and this ends up being c and so we have shown that this second observer will report the same thing as the first observer when they are talking about the speed of light.