Question
Suppose a particle called a kaon is created by cosmic radiation striking the atmosphere. It moves by you at , and it lives when at rest relative to an observer. How long does it live as you observe it?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 28, Problem 4 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
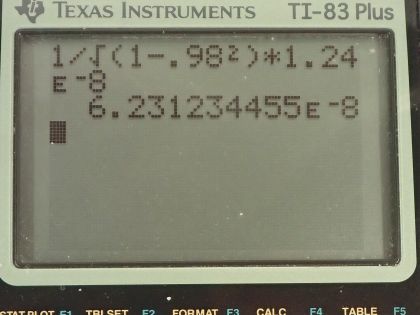
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A kaon particle is moving at 0.980 times the speed of light c; when an observer is at rest with respect to the particle, they measure a lifetime for it of 1.24 times 10 to the minus 8 seconds and because this time is measured at rest with respect to the particle, it's called the proper time, t naught. So Δt—the time measured by the person watching the things zip by— equals the Lorentz factor γ times the proper time. So that's 1 over the square root of 1 minus v squared over c squared times Δt naught and that's 1 over the square root of 1 minus 0.980 times c all squared over c squared times 1.24 times 10 to the minus 8 seconds and that is 6.23 times 10 to the minus 8 seconds. This is the time measured by an Earth-based observer watching the kaon particle zip past.