Question
The purpose of producing (usually by neutron activation of natural molybdenum, as in the preceding problem) is to produce . Using the rules, verify that the decay of produces . (Most
nuclei produced in this decay are left in a metastable excited state denoted .)
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 32, Problem 3 (Problems & Exercises)
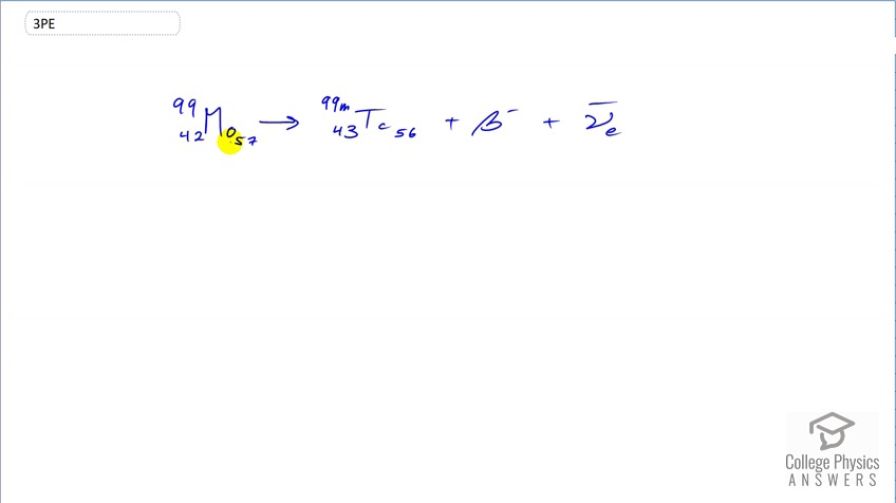
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to verify that the beta decay of molybdenum produces technetium. So beta decay means that a neutron in the nucleus turns into a proton and an electron. So we expect the atomic number 42 for molybdenum to change into 43 with the addition of a proton and in order for charge to be conserved, an electron is also produced on this right-hand side. Now the atomic mass of 99 will not change because there are still the same number of nucleons, the neutron just turned into a proton and so there are still 99 nucleons. The letter m here you can ignore it; it just means that this is a metastable state of technetium it's just an excited nuclide. In any case, it's still an atomic mass of 99. So we have shown that that's what happens when molybdenum has beta decay, it turns into technetium because that's the element with a atomic number one greater than that of molybdenum; 43 versus 42. and we also have this electron anti-neutrino produced in order to conserve the electron family number seeing as this electron has been created which has an electron family number of plus 1 and so we need an electron anti-neutrino with a compensating electron family number of negative 1 in order to have a total of zero on this right-hand side as we started with zero on the left.